Ausbreitung gaußscher Strahlen

Das ist Abschnitt 2.1 des Leitfadens für Laseroptiken.

In vielen Laseroptikanwendungen wird davon ausgegangen, dass der Laserstrahl gaußförmig mit einem Strahlungsprofil ist, das einer idealen gaußschen Verteilung entspricht. In der Realität weichen jedoch alle Laserstrahlen geringfügig vom idealen Gaußverhalten ab. Der Faktor M², die so genannte Strahlkennzahl, vergleicht die Leistung eines realen Laserstrahls mit einem beugungsbegrenzten gaußschen Strahl.¹ Leistung eines realen Laserstrahls mit einem beugungsbegrenzten gaußschen Strahl.1 Gaußsche Strahlungsprofile sind symmetrisch zur Mitte des Strahls und werden mit zunehmendem Abstand von der Mitte des Strahls senkrecht zur Ausbreitungsrichtung kleiner (Abbildung 1). Diese Verteilung wird durch Gleichung 1beschrieben.²:

(1)$$ I \! \left( r \right) = I_0 \exp{\left( \frac{-2 r^2}{w \! \left( z \right)^2} \right)} = \frac{2P}{\pi w \! \left( z \right)^2} \exp{\left( \frac{-2 r^2}{w \! \left( z \right)^2} \right)} $$

In Gleichung 1 ist I₀ die maximale Strahlungsintensität in der Mitte des Strahls, r ist der radiale Abstand von der Achse, w(z) ist der Radius des Laserstrahls, an dem die Strahlungsintensität 1/e² (13.5 %) von I₀ beträgt, z ist die zurückgelegte Entfernung von der Ebene, bei der die Wellenfront flach ist, und P ist die Gesamtleistung des Strahls.

Abbildung 1: Die Taille eines gaußschen Strahls ist als die Stelle definiert, an der die Strahlungsintensität 1/e<sup>2</sup> (13.5%) des Maximalwerts beträgt.

Abbildung 1: Die Taille eines gaußschen Strahls ist als die Stelle definiert, an der die Strahlungsintensität 1/e² (13.5%) des Maximalwerts beträgt.

Dieses Strahlungsprofil bleibt jedoch bei der Ausbreitung des Strahls im Raum nicht konstant, da w(z) von z abhängt. Beugungsbedingt konvergiert und divergiert ein gaußscher Strahl, wobei er in einem bestimmten Bereich, der so genannten Strahltaille (w₀), den Minimalwert des Strahldurchmessers erreicht. Der Strahl konvergiert und divergiert gleichermaßen auf beiden Seiten der Strahltaille um den Divergenzwinkel θ (Abbildung 2). Strahltaille und Divergenzwinkel werden von der Achse aus gemessen. Deren Beziehung ist in Gleichung 2 und Gleichung 3²ersichtlich:

(2)$$ w_0 = \frac{\lambda}{\pi \theta} $$

(3)$$\theta = \frac{\lambda}{\pi w_0} $$

In den obigen Gleichungen ist λ die Wellenlänge des Lasers und θ ist eine Fernfeldapproximation. Daher stellt θ Divergenz des Strahls in der Nähe der Strahltaille nicht exakt dar. Die Approximation wird jedoch mit zunehmender Entfernung von der Strahltaille immer genauer. Wie in Gleichung 3ersichtlich, führt eine kleine Strahltaille zu einem größeren Divergenzwinkel, während eine große Strahltaille zu einem kleineren Divergenzwinkel, d. h. einem stärker kollimierten Strahl, führt. Dies erklärt, warum Strahlaufweiter durch Vergrößerung des Strahldurchmessers die Strahldivergenz verringern können.

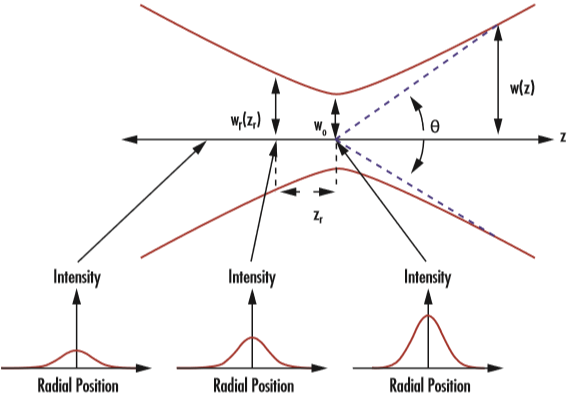
Abbildung 2: Gaußsche Strahlen werden durch Strahltaille, Rayleighlänge und Divergenzwinkel definiert.

Abbildung 2: Gaußsche Strahlen werden durch Strahltaille (w₀), Rayleighlänge (z_R) und Divergenzwinkel (θ) definiert.

Die Änderung des Strahldurchmessers im Bereich der Strahltaille ist definiert durch:

(4)$$ w \! \left( z \right) = w_0 \sqrt{1 + \left( \frac{\lambda z}{\pi w_0 ^2} \right)^2} $$

Die Rayleighlänge eines gaußschen Strahls ist definiert als der Wert von z, an dem sich die Querschnittsfläche des Strahls verdoppelt hat. Dies ist der Fall, wenn w(z) so groß wie √2 w₀ist. Mit Gleichung 4 kann die Rayleighlänge (z_R) ausgedrückt werden als:

(5)$$ z_R = \frac{\pi w_0 ^2}{\lambda } $$

Damit kann die Abhängigkeit von w(z) von z_Rangegeben werden als:

(6)$$ w \! \left( z \right) = w_0 \sqrt{1 + \left( \frac{\lambda z}{\pi w_0 ^2} \right)^2} = w_0 \sqrt{1 + \left( \frac{z}{z_R} \right)^2} $$

Die Wellenfront des Lasers ist an der Strahltaille eben und nähert sich dieser Form wieder an, je größer die Entfernung vom Bereich der Strahltaille wird. Dies liegt daran, dass sich der Krümmungsradius der Wellenfront einem unendlichen Wert nähert. Der Krümmungsradius der Wellenfront sinkt von unendlich an der Strahltaille auf einen Minimalwert bei der Rayleighlänge und steigt dann in großer Entfernung vom Laser wieder auf unendlich (Abbildung 3). Dies gilt für beide Seiten der Strahltaille.³

Abbildung 3: Die Krümmung der Wellenfront eines gaußschen Strahls ist nahezu Null, wenn sie sich sehr nah an und sehr weit weg von der Strahltaille befindet.

Passende Produkte

Beeinflussung von gaußschen Strahlen

In vielen Laseroptiksystemen muss der Originallaserstrahl manipuliert werden und es kann nicht einfach der „Rohstrahl“ eingesetzt werden. Dies kann durch optische Komponenten wie Linsen, Spiegel, Prismen usw. erfolgen. Nachstehend werden einige gebräuchliche Beeinflussungsmöglichkeiten für gaußsche Strahlen beschrieben.

Die Linsengleichung für gaußsche Strahlen

Das Verhalten einer idealen dünnen Linse kann durch folgende Gleichung beschrieben werden²:

(7)$$ \frac{1}{s'} = \frac{1}{s} + \frac{1}{f} $$

In Gleichung 7ist s’ der Abstand von der Linse zum Bild, s der Abstand von der Linse zum Objekt und f die Brennweite der Linse. Wenn sich Objekt und Bild auf gegenüberliegenden Seiten der Linse befinden, ist s negativ und s’ positiv. Diese Gleichung vernachlässigt die Dicke einer tatsächlichen Linse und ist daher nur eine einfache Näherung des wirklichen Verhaltens (Abbildung 4). Die Linsengleichung kann auch in einer dimensionslosen Form geschrieben werden, indem beide Seiten der Gleichung mit f multipliziert werden:

(8)$$ \frac{f}{s'} = \frac{f}{s} + 1 \text{ or } \frac{1}{\left( \frac{s'}{f} \right)} = \frac{1}{\left( \frac{s}{f} \right)} + 1 $$

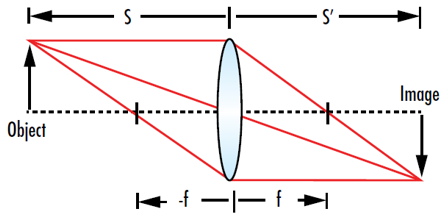
Abbidlung 4: Die Linsengleichung ermöglicht die Bestimmung der Position eines Bildes (s’), wenn der Abstand von der Linse zum Objekt (s) und die Brennweite der Linse (f) bekannt sind.

Abbildung 4: Die Linsengleichung ermöglicht die Bestimmung der Position eines Bildes (s’), wenn der Abstand von der Linse zum Objekt (s) und die Brennweite der Linse (f) bekannt sind.

Neben der Beschreibung von Bildverarbeitungsanwendungen kann die Linsengleichung auch für die Fokussierung eines gaußschen Strahls verwendet werden, indem die Taille des Eingangsstrahls als Objekt und die Taille des Ausgangsstrahls als Bild behandelt werden. Gaußsche Strahlen bleiben auch nach Durchgang durch eine ideale Linse ohne Aberration gaußförmig. Im Jahr 1983 wurde von Sidney Self eine Version der Linsengleichung entwickelt, die die gaußsche Ausbreitung berücksichtigt⁴:

(9)$$ \boxed{ \frac{1}{s'} = \frac{1}{ s + \frac{z_R ^2}{\left( s + f \right)}} + \frac{1}{f} } $$

Die Gesamtstrecke vom Laser zum fokussierten Spot wird durch Addition des Absolutwerts von s zu s’ berechnet. Gleichung 9 kann auch in einer dimensionslosen Form geschrieben werden, indem beide Seiten mit f multipliziert werden:

(10)$$ \frac{f}{s'} = \frac{1}{\left( \frac{s}{f} \right) + \frac{\left( \frac{z_R}{f} \right)^2}{\left( \frac{s}{f} + 1 \right)} } + 1 $$

Diese Gleichung nähert sich der Linsengleichung für dünne Linsen an, wenn sich z_R/f dem Wert 0 nähert, sodass die Linsengleichung für dünne Linsen für Linsen mit einer großen Brennweite verwendet werden kann. Mithilfe von Gleichung 9 und 10 kann die Position der Strahltaille nach Durchgang durch die Linse ermittelt werden (Abbildung 5).

Abbildung 5: Bei der Refokussierung eines gaußschen Strahls ist die Eingangstaille das „Objekt“ und die Ausgangstaille ist das „Bild“.

Ein Diagramm der normalisierten Bildweite (s’/f) über der normalisierten Objektweite (s/f) veranschaulicht die möglichen Ausgangstaillenpositionen bei einer gegebenen normalisierten Rayleighlänge (z_R/f) (Abbildung 6). Dieses Diagramm zeigt, dass durch eine Linse fokussierte gaußsche Strahlen einige wesentliche Unterschiede im Vergleich zur konventionellen Abbildung mit dünnen Linsen aufweisen. Die Abbildung von gaußschen Strahlen weist im Gegensatz zur konventionellen Abbildung mit dünnen Linsen eine minimale und maximale mögliche Bildweite auf. Die maximale Bildweite eines refokussierten gaußschen Strahls tritt bei einer Objektweite von -(f + z_R) auf, nicht –f. An dem Punkt im Diagramm, an dem s/f gleich –1 und s’/f gleich 1 ist, befindet sich die Ausgangstaille am bildseitigen Brennpunkt der Linse, wenn sich die Eingangstaille am objektseitigen Brennpunkt einer Sammellinse befindet.

Abbildung 6: Die Kure, bei der z<sub>R</sub>/f=0 ist, entspricht der konventionellen Linsengleichung. Die Kurven, bei denen z<sub>R</sub>/f>0 zeigen, dass es bei der gaußschen Abbildung eine minimale und maximale Bildweite gibt, die durch die Rayleighlänge festgelegt werden.

Abbildung 6: Die Kurve, bei der z_R/f=0 ist, entspricht der konventionellen Linsengleichung. Die Kurven, bei denen z_R/f>0 zeigen, dass es bei der gaußschen Abbildung eine minimale und maximale Bildweite gibt, die durch die Rayleighlänge festgelegt werden.

Um die Strahltaille und die Rayleighlänge zu verstehen, nachdem der Strahl die Linse durchlaufen hat, muss die Vergrößerung des Systems (α) bekannt sein. Diese ist:

(11)$$ \alpha = \frac{w'_0}{w_0} = \frac{1}{\sqrt{\left(1 - \frac{s}{f} \right)^2 + \left( \frac{z_R}{f} \right)^2}} $$

Dabei ist w₀ die Strahltaille vor der Linse und w₀’ die Strahltaille hinter der Linse. Die Linsengleichung für gaußsche Strahlen kann dann so umgeschrieben werden, dass sie die Rayleighlänge des Strahls hinter der Linse (z_R') enthält:

(12)$$ \boxed{ \frac{1}{ s' + \frac{{z'}_R ^2}{\left( s' - f \right)} } = \frac{1}{s} + \frac{1}{f} } $$

Die obige Gleichung versagt, wenn sich die Linse an der Strahltaille befindet (s=0). Um Größe und Position der Strahltaille zueinander in Beziehung zu setzen, kann der Kehrwert der Vergrößerungskonstante im Quadrat verwendet werden³:

(13)$$ \frac{1}{\alpha ^2} = \frac{ \left| s \right| - f}{s' -f} = \left( \frac{w_0}{w'_0} \right)^2 $$

Fokussierung eines gaußschen Strahls auf einen Spot

In vielen Anwendungen, z. B. Lasermaterialbearbeitung oder Laserchirurgie, muss ein Laserstrahl auf den kleinstmöglichen Spot fokussiert werden, um die Intensität zu maximieren und den erhitzten Bereich zu minimieren. In solchen Fällen muss w₀' minimiert werden (Abbildung 7). Um festzustellen, wie eine Minimierung der Ausgangsstrahltaille möglich ist, kann eine modifizierte Version von Gleichung 13 verwendet werden³:

(14)$$ \frac{\left( \left| s \right| -f \right)^2}{f^2 - \left( \frac{{w'}_0}{\theta} \right)^2 } = \left( \frac{w_{0}}{{w'}_0} \right)^2 $$

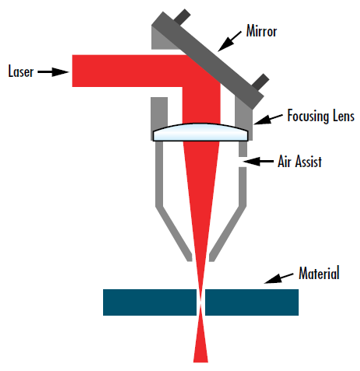
Abbildung 7: Die Fokussierung eines Laserstrahls auf die kleinstmögliche Größe ist für eine Vielzahl von Anwendungen wie diese Laserschneideeinrichtung von entscheidender Bedeutung.

Nach Multiplikation beider Seiten mit dem Nenner der linken Seite der Gleichung und anschließender Multiplikation beider Seiten mit (w₀')² wird Gleichung 14 zu:

(15)$$ \left( \left| s\right| -f \right)^2 = f^2 \left( \frac{w_0}{w'_0} \right)^2 - \left( \frac{w_0}{\theta} \right)^2 = f^2 \left( \frac{w_0}{w'_0} \right)^2 - z_R ^2 $$

(16)$$ \left( w'_0 \right) ^2 \left[ \left( \left| s \right| - f \right)^2 + z_R ^2 \right] = f^2 w_0 ^2 $$

Durch Auflösung nach w₀' ergibt sich:

(17)$$ \boxed{ w'_0 = w_0 \frac{f}{\sqrt{\left( \left| s \right| - f \right) ^2 + z_R ^2}} = \alpha w_0 } $$

(18)$$ \boxed{ \alpha = \frac{f}{\sqrt{\left( \left| s \right| -f \right)^2 + z_R ^2}} } $$

Die fokussierte Strahltaille kann durch Verringerung der Brennweite der Linse und |s| − f minimiert werden. Die Glieder neben w₀ in Gleichung 17 werden in einer anderen Form als Vergrößerungskonstante α definiert, um die Werte des Eingangsstrahls nach dem Durchgang durch die Linse mit dem Ausgangsstrahl zu vergleichen Abbildung 8).³

(19)$$ \theta ' = \frac{\lambda}{\pi w'_0} = \frac{\lambda}{\pi \alpha w_0} = \frac{\theta}{\alpha} $$

(20)$$ z'_R = \frac{w'_0}{\theta '} = \frac{\alpha w_0}{\left( \frac{\theta}{\alpha} \right)} = \alpha ^2 z_R $$

(21)$$ \boxed{ s' = f + \alpha ^2 \left( \left| s \right| - f \right)} $$

Bei einer Vergrößerung von 2 ist die Ausgangsstrahltaille doppelt so groß wie die Eingangsstrahltaille und die Ausgangsdivergenz halb so groß wie die Eingangsstrahldivergenz.

Abbildung 8: Bei einer Vergrößerung von 2 ist die Ausgangsstrahltaille doppelt so groß wie die Eingangsstrahltaille und die Ausgangsdivergenz halb so groß wie die Eingangsstrahldivergenz.

Es gibt zwei Grenzfälle, die die Berechnung von Größe und Position der Ausgangsstrahltaille vereinfachen: wenn s sehr viel kleiner als z_R oder sehr viel größer als z_R ist.³ Wenn sich die Linse innerhalb der Rayleighlänge des Lasers befindet, gilt s << z_R und (|s| − f)² < z_R². Dadurch wird Gleichung 18 vereinfacht zu:

(22)$$ \alpha = \frac{f}{z_R} = \frac{f \theta}{w_0} $$

Dadurch werden auch die Berechnungen für Taille, Divergenz, Rayleighlänge und Taillenposition des Ausgangsstrahls vereinfacht:

(23)$$ \theta ' = \frac{\theta}{\alpha} = \frac{ \theta w_0}{f \theta} = \frac{w_0}{f} $$

(24)$$ z_R ' = \alpha ^2 z_R = \frac{f^2}{z_R ^2} z_R = \frac{f^2}{z_R} $$

(25)$$ \boxed{ w'_0 = \alpha w_0 = f \theta } $$

(26)$$ \boxed{ s' = f + \alpha^2 \left( \left| s \right| - f \right) = f + \frac{ \left| s \right| f^2}{z_R ^2} \approx f } $$

Wenn s >> z_R, ist, stimmt der Abstand von der Linse zum fokussierten Spot mit der Brennweite der Linse überein.

Im anderen Grenzfall befindet sich die Linse weit außerhalb der Rayleighlänge und s ist sehr viel größer als z_R. Dadurch wird Gleichung 18 wie folgt vereinfacht:

(27)$$ \alpha = \frac{f}{\left| s \right|} $$

Der Durchmesser der Ausgangsstrahltaille beträgt dann:

(28)$$ w'_0 = \frac{f w}{ \left| s \right|} $$

Analog zum Fall s << z_Rwerden auch die Berechnungen für Ausgangsstrahltaille, Divergenz, Rayleighlänge und Strahltaillenposition vereinfacht:

(29)$$ \theta ' = \frac{\theta}{\alpha} = \frac{\left| s \right| \theta }{f} $$

(30)$$ z'_R = \alpha^2 z_R = \frac{f^2 z_R}{s^2} $$

(31)$$ \boxed{ w'_0 = \alpha w_0 = \frac{fw_0}{\left| s \right|} } $$

(32)$$ \boxed{ s' = f + \alpha ^2 \left( \left| s \right| - f \right) = f + \frac{\left( \left| s \right| - f \right) f^2}{s^2} = f + \frac{f^2}{ \left| s \right|} \approx f } $$

Wenn s >> z_R ist, stimmt der Abstand von der Linse zum fokussierten Spot mit der Brennweite der Linse überein.

Beide Ergebnisse sind intuitiv einleuchtend, da die Wellenfront des Strahls an der Strahltaille und sehr weit weg von der Strahltaille annähernd eben ist. An diesen Stellen ist der Strahl nahezu perfekt kollimiert (Abbildung 9). Laut der standardmäßigen Gleichung für dünne Linsen würde ein kollimierter Eingangsstrahl eine Bildweite gleich der Brennweite der Linse aufweisen.

Abbildung 9: Der fokussierte Spot eines gaußschen Strahls nach Durchgang durch eine Linse befindet sich am Brennpunkt der Linse, wenn sich die Eingangsstrahltaille sehr nah bei oder sehr weit weg von der Linse befindet. Dies liegt daran, dass der Eingangsstrahl an diesen Stellen annähernd kollimiert ist.

Gaußsche Brennpunktverschiebung

Gegen die eigene Intuition ist die Intensität eines fokussierten Strahls in einem Ziel in einer festen Entfernung (L) von der Linse nicht maximal, wenn sich die Taille am Ziel befindet. Die Intensität am Ziel ist tatsächlich maximal, wenn sich die Taille vor dem Ziel befindet (Abbildung 10). Dieses Phänomen wird gaußsche Brennpunktverschiebung genannt.

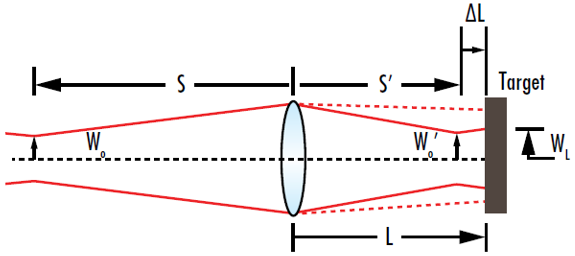
Abbildung 10: Der minimale Strahlradius am Ziel tritt auf, wenn sich die Taille des fokussierten Strahls an einer bestimmten Stelle vor dem Ziel befindet, und nicht, wenn sich die fokussierte Taille am Ziel befindet.

Die ausführliche Ableitung wird in diesem Text nicht behandelt. Der Strahlradius am Ziel kann jedoch durch den folgenden Ausdruck beschrieben werden⁴:

(33)$$ w_L = \frac{w_0}{z_R} \left[ f^2 - 2 \left( \left| s \right| - f \right) \left( L - f \right) + \left( \frac{L-f}{\alpha} \right)^2 \right] $$

Ableitung von Gleichung 34 nach der Brennweite der Fokussierlinse und Auflösung nach f wenn ^d⁄_df [w_L (f )] = 0 ist, zeigt die Brennweite der Linse mit dem minimalen Strahlradius und daher der größten Intensität am Ziel auf.

(34)$$ \frac{ \text{d} }{ \text{d}f } \left[ w_L \! \left( f \right) \right] = \frac{w_0}{z_R} \left[ 2f + \left( \left| s \right| -f \right) +2 \left( L - f \right) - \frac{2 \left( L - f \right)}{\alpha ^2} \right] $$

(35)$$ \frac{ \text{d} }{ \text{d}f } \left[ w_L \! \left( f \right) \right] = 0 \text{ when } f = \left( \frac{1}{\left| s \right| + \frac{z_R ^2}{\left| s \right|}} + \frac{1}{L} \right) ^{-1} $$

Wenn sich |s| null oder unendlich nähert, gilt ^d⁄_df [w_L (f )] = 0 bei f = L. In beiden Fällen ist der Eingangsstrahl annähernd kollimiert. Daraus folgt, dass der kleinste Strahlradius am Brennpunkt der Linse auftritt.

Kollimation eines gaußschen Strahls

Es ist nicht möglich, einen wirklich kollimierten Strahl mit einer Divergenz von 0 zu erreichen. Es ist jedoch möglich, durch Minimieren der Divergenz oder Maximieren des Abstands zwischen dem Beobachtungspunkt und der nächstliegenden Strahltaille einen annähernd kollimierten Strahl zu erreichen. Da die Ausgangsdivergenz umgekehrt proportional zur Vergrößerungskonstanten αist, erreicht die Ausgangsdivergenz ein Minimum, wenn |s| = f ist (Abbildung 11).

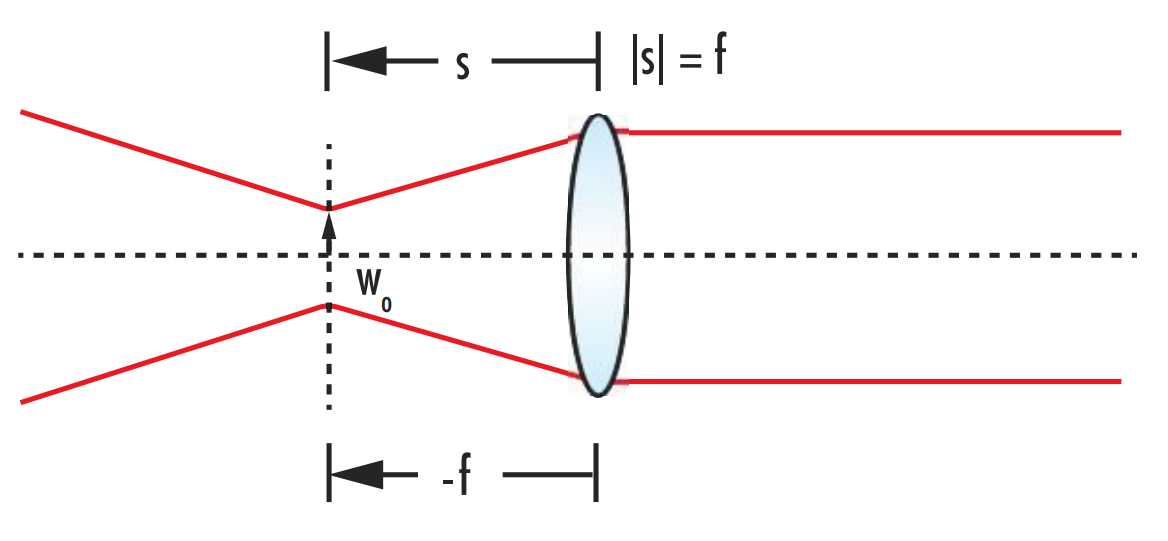
Abbildung 11: Zur Kollimation eines gaußschen Strahls muss der Abstand von der Strahltaille zur Kollimatorlinse der Brennweite der Linse entsprechen.

Referenzen

Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, January 1983.
O'Shea, Donald C. Elements of Modern Optical Design. Wiley, 1985.
Self, Sidney A. “Focusing of Spherical Gaussian Beams.” Applied Optics, vol. 22, no. 5, Jan. 1983.
Katz, Joseph, and Yajun Li. “Optimum Focusing of Gaussian Laser Beams: Beam Waist Shift in Spot Size Minimization.” Optical Engineering, vol. 33, no. 4, Apr. 1994, pp. 1152–1155., doi:10.1117/12.158232.

Vorheriger Abschnitt Nächster Abschnitt

Weiterführende Informationen

Knowledge Center/ Anwendungshinweise/ Anwendungshinweise/ Ausbreitung gaußscher Strahlen