eo_logo
 
Produkt in den Warenkorb gelegt

 
Strahlversatzrechner

Alle Technischen Tools

Einfallswinkel, θ (Grad):

Dicke der Platte, t (mm):

Brechungsindex des Mediums, n:

Strahlversatz, s (mm): --     

Versatz der zweiten Reflexion, x (mm): --     

Brennweitenrechner
$$ s = t \cdot \sin{\theta} \left( 1 - \frac{\cos{\theta}}{\sqrt{n^2 - \sin^2{\theta}}} \right) $$
$$ x = \frac{t \cdot \sin{\left( 2 \theta \right)}}{\sqrt{n^2 - \sin^2{\theta}}} $$
s Strahlversatz
x Versatz der zweiten Reflexion
θ Einfallswinkel zwischen Strahl und der Normalen
t Dicke der Platte
n Brechungsindex des Mediums

Bitte beachten Sie: Dieser Rechner gilt nur innerhalb der folgenden Bereiche: t > 0 mm, 0° < θ < 90°, n > 0. Verwenden Sie bitte die amerikanische Zahlenschreibweise und nicht die europäische (z. B. „2.5“ statt „2,5“ für die Zahl „zweieinhalb“).

Beschreibung

Bestimmen Sie den Versatz eines kollimierten Strahls, der auf ein gekipptes, planparalleles Fenster fällt. Der Versatz hängt vom Einfallswinkel, der Dicke der Platte und dem Brechungsindex der Platte ab. Der Rechner bestimmt außerdem den Versatz der zweiten Reflexion, die entsteht, weil eine geringe Menge des Strahls an der Glas-Luft-Grenze der Platte zurückreflektiert wird.

Der Ausgangsstrahl ist parallel zum Eingangsstrahl und die Vergrößerung bleibt bei einer Abbildung durch eine planparallele Platte konstant.

Beispiel

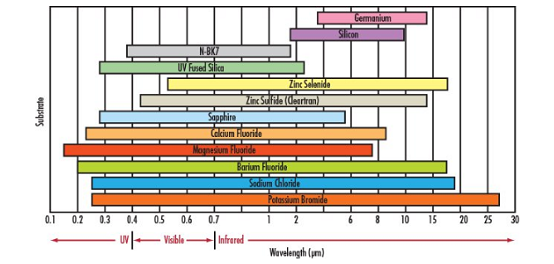
Frage: Wie groß ist der Versatz des Strahls und der zweiten Reflexion, wenn der Strahl mit einem Einfallswinkel von 15 Grad durch eine 10 mm dicke Platte aus N-BK7 fällt?

Antwort: Der Strahlversatz und der Versatz der zweiten Reflexion kann bestimmt werden durch:

$$ s = \left( 10 \text{ mm} \right) \sin{\left( 15° \right)} \left( 1 - \frac{\cos{\left( 15° \right)}}{\sqrt{1,517^2 - \sin^2{\left(15° \right)}}} \right) = 0,916 \text{ mm} $$
$$ x = \frac{\left( 10 \text{ mm} \right) \sin{\left( 2 \cdot 15° \right)}}{\sqrt{1,517^2 - \sin^2{\left( 15° \right)}}} = 3,499 \text{ mm} $$

Der Versatz des Strahls beträgt 0,916 mm und der Versatz der zweiten Reflexion 3,499 mm.

Weiterführende Informationen

 Anwendungshinweis
Grundlagen optischer Fenster
Grundlagen optischer Fenster
 Anwendungshinweis
Optisches Glas
Optisches Glas

Passende Produkte: Optische Fenster

Alle ansehen
 
Vertrieb & Beratung
 
weitere regionale Telefonnummern
 LIVE-CHAT
Einfaches
ANGEBOTSTOOL
Geben Sie zum Starten die Produktnummer ein.
Bleiben Sie informiert | Industrie-Trends, neue Produkte, Rabatte und technische Informationen  Jetzt anmelden
Über uns Über unsMessen Regionale Niederlassungen Karriere Pressemeldungen Fallstudien Compliance TECHSPEC®Firmen-Partnerschaften Kontakt
Kundenservice VersandRücksendungHilfeFeedback geben Fertigung bei Präzisions Optik Filter LaserOptik Objektive
Rabatte & Programme Alle Rabattprogramme Vision Integration Partners Rabatte für große StückzahlenRabattprogramm für Forschung & Lehre Educational Award Reduzierte Produkte Edmund Scientific
Kataloge Alle Kataloge Digitale Kataloge Katalog-Einstellungen Starten Sie jetzt Ihre Stellensuche bei EO!

Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK

DATENSCHUTZRICHTLINIE | COOKIE POLICY | AGB | AGB FÜR B2C | IMPRESSUM | BARRIEREFREIHEIT

Die Edmund Optics GmbH Deutschland fungiert als Handelsvermittler für die Edmund Optics Ltd. in Großbritannien.
Vertragspartner ist die Edmund Optics Ltd. in Großbritannien.