Rechner für Kugellinsen

Material der Kugellinse:

n: --

D:

d:

EFL (mm): --     
BFL (mm): --     
NA: --     

$$ \text{EFL} = \frac{n \, D}{4 \left( n - 1 \right)} $$

$$ \text{BFL} = \text{EFL} - \frac{D}{2} $$

$$ \text{NA} = \frac{2 d \left( n - 1 \right) }{n \, D} $$

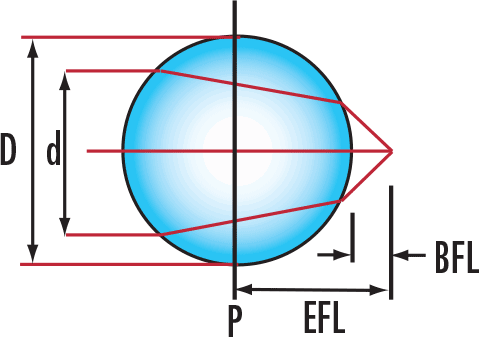
EFL	Effektive Brennweite
BFL	Hintere Brennweite
NA	Numerische Apertur

n	Brechungsindex
D	Durchmesser der Kugellinse
d	Durchmesser des einfallenden Lichts

Verwenden Sie bitte die amerikanische Zahlenschreibweise und nicht die europäische (z. B. „2.5“ statt „2,5“ für die Zahl „zweieinhalb“).

Beschreibung

Bestimmen Sie die effektive Brennweite, die hintere Brennweite und die effektive numerische Apertur einer Kugellinse anhand ihres Durchmessers, Brechungsindex und des Durchmessers des kollimierten Eingangsstrahls, der auf die Kugellinse trifft. Die effektive numerische Apertur der Anwendung kann nur berechnet werden, wenn der Nutzer den Strahldurchmesser kennt. Wenn Kugellinsen eingesetzt werden, um Licht aus einer Faser in einen Laser oder eine andere Faser zu koppeln, ist es besonders hilfreich die numerische Apertur zu kennen.