Bildgebungselektronik 101: Kameraauflösung und ihr Einfluss auf die Bildqualität

Die Kameraauflösung und der Kontrast spielen eine wichtige Rolle, sowohl für die Optik als auch die Elektronik eines Bildgebungssystems. Kameraauflösung und Kontrast sind vielleicht die offensichtlichsten optischen Parameter, aber auch Pixelzahl und Pixelgröße, Zeilenzahl, Kamera-MTF, Nyquist-Grenzwert, Pixeltiefe/Grauskala, Dynamikbereich und Signal-Rausch-Verhältnis beeinflussen die Qualität des Bildes, das ein Benutzer aufnehmen will. Mit unseren technischen Tipps zu allen wichtigen Parametern können alle Anwender von Bildgebungssystemen, egal ob Einsteiger oder Experte, mehr über die Kameraauflösung als Teil der Bildgebungselektronik eines Systems erfahren.

PIXELZAHL UND PIXELGRÖSSE

Um den Einfluss von Pixelzahl und -größe auf das Gesamtsystem zu verstehen, betrachten wir beispielhaft die Allied Vision Stingray F-145 mit Firewire-Anschluss. Die F-145 enthält einen Sony ICX285-Sensor mit 1392 x 1040 Pixeln (horizontal x vertikal) auf einer Fläche von 9,0 mm x 6,7 mm. Wenn man sich das Bildfeld als Rechteck vorstellt, das in 1392 x 1040 Quadrate unterteilt ist (Abb.1), entspricht das kleinste noch auflösbare Detail zwei dieser Quadrate oder Pixel (Abb.2). Techniktipp Nr. 1: Je mehr Pixel für ein vorgegebenes Bildfeld zur Verfügung stehen, umso besser ist die Auflösung. Eine große Pixelzahl erfordert jedoch entweder einen größeren Sensor oder kleinere Einzelpixel. Deshalb Techniktipp Nr. 2: Bei Verwendung eines größeren Sensors mit mehr Pixeln ändert sich entweder das Bildfeld oder die Vergrößerung des Objektivs muss neu gewählt werden. Wenn dagegen kleinere Pixel verwendet werden, dann kann die Systemauflösung eventuell durch die endliche Auflösung des Objektivs begrenzt werden. Haupgründe dafür sind in erster Linie das Design des Objektivs oder das generelle Beugungslimit.

Von der Anzahl der Pixel hängt auch die Bildwiederholfrequenz der Kamera ab. Wenn jedes Pixel beispielsweise 8 Bit Informationen enthält, müssen diese zur Bildrekonstruktion auch übertragen werden. Techniktipp Nr. 3: Je mehr Pixel ein Sensor besitzt, umso höher ist die Kameraauflösung, aber umso niedriger wird auch die Bildwiederholrate. Wenn sowohl hohe Einzelbildfrequenzen als auch hohe Auflösung, d.h. viele Pixel, erwünscht sind, steigen Systempreis und Komplexität schnell an, oft auch überproportional zur Pixelzahl.

Abb.1: Pixel auf einem Kamerasensor

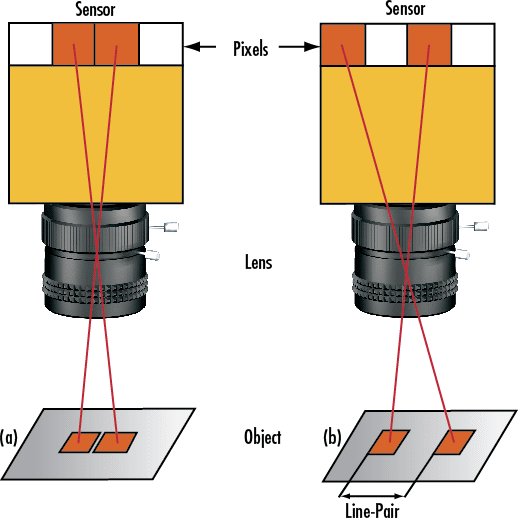
Abb.2: Nicht aufgelöstes Pixelpaar (a) und aufgelöstes Pixelpaar (b)

BILDZEILENZAHL

Bei analogen CCD-Kameras wird die Zahl der TV-Zeilen (TVL) oft als Maß für die Bewertung der Auflösung verwendet. Die TVL-Spezifikation bewertet die Auflösung mit einem Streifenmuster mit Linien in gleichmäßigem Abstand. Das Testbild wird so vergrößert, dass es das Bildfeld ausfüllt. Die Zahl der TV-Zeilen ist dann die Summe aller dargestellten Balken und Zwischenräume. Die Gleichungen 1 und 2 erlauben die einfache Berechnung der horizontalen (H) und vertikalen (V) Bildzeilenzahl. In Gleichung 1 ist ein Normalisierungsfaktor enthalten, der das Seitenverhältnis des Sensors von 4:3 berücksichtigt. Abbildung 3 zeigt ein vom IEEE zugelassenes Testbild zur Bestimmung der Bildzeilenzahl eines Systems.

Abb.3: Vom IEEE zugelassenes Testbild zur Bestimmung der Bildzeilenzahl (TVLs)

MODULATIONSTRANSFERFUNKTION (MTF)

Die effektivste Möglichkeit zur Definition der Kameraauflösung ist deren Modulationstransferfunktion (MTF). Die Modulationstransferfunktion erlaubt es, Kontrast und Auflösung bei der Bestimmung der Gesamteigenschaften eines Sensors zu berücksichtigen. Eine nützliche Eigenschaft der Modulationstransferfunktion ist die Möglichkeit der Multiplikation. Die Modulationstransferfunktionen aller Komponenten (Objektiv, Kamerasensor, Display usw.) können miteinander multipliziert werden, um die Kennlinie des Gesamtsystems zu erhalten (Abb.4).

Abb.4: Die Modulationstransferfunktion des Systems ist das Produkt aus den Modulationstransferfunktionen aller einzelnen Komponenten

Die MTF berücksichtigt nicht nur die räumliche Auflösung mit der Zahl der Pixel pro Millimeter, sondern auch den Roll-Off-Effekt, der bei hohen Raumfrequenzen aufgrund der gegenseitigen Störungen der Pixel und des endlichen Füllfaktors auftritt. Techniktipp Nr. 4: Ein Sensor hat bei einer Raumfrequenz, die dem Kehrwert seiner Pixelgröße entspricht, niemals einen hundertprozentigen Kontrast. Eine vollständige Diskussion über die Modulationstransferfunktion und deren Bedeutung finden Sie im Anwendungshinweis Modulationstransferfunktion.

NYQUIST-GRENZWERT

Der absolute Grenzwert für die Auflösung eines Sensors wird durch den Nyquist-Grenzwert bestimmt. Definiert ist dieser als die Hälfte der Abtastfrequenz, d.h. die Anzahl der Pixel pro Millimeter (Gleichung 3). Der Sensor Sony ICX285 ist beispielsweise ein monochromer CCD-Sensor mit einer horizontalen aktiven Fläche von 9 mm mit 1392 horizontalen Pixeln mit einer Größe von jeweils 6,45 μm. Dies entspricht einer horizontalen Abtastfrequenz von 155 Pixeln/mm (1392 Pixel/9 mm = 1 / 0,00645 Pixel/mm = 155 Pixel/mm). Der Nyquist-Grenzwert hierfür ergibt sich zu 77,5 lp/mm. Für Kanten und einfache geometrische Formen gibt es Bildverarbeitungsverfahren, wie das Subpixel-Sampling, die durch statistische Extrapolation erlauben, den Nyquist Grenzwert zu überschreiten. Beim Nyquist-Grenzwert ist der Kontrast für eine konstant einfallende Rechteckwelle phasenabhängig. Wenn die Welle sich mit den Pixeln deckt, dann ist jeweils ein Pixel "an", einer "aus". Ist die Welle dagegen um eine halbe Wellenlänge verschoben, dann zeigen beide Pixel dieselbe Intensität. Ist die Welle nicht sauber zu den Pixeln ausgerichtet, dann hängt die Phasenlage vom Ort ab und es kommt zu Schwebungen und damit zu Artefakten im Bild. Es ist daher üblich, den Kell-Faktor (circa 0,7) einzuführen, der die Abweichung zwischen der Nyquist-Frequenz und derjenigen Frequenz angibt, bei der diese Schwebungen nicht auftreten. Vor allem aber kompensiert der Kell-Faktor auch den Abstand zwischen den einzelnen Pixeln, der bisher nicht berücksichtigt wurde. Techniktipp Nr. 5: Eine Abtastung von Raumfrequenzen oberhalb der Nyquist-Grenzfrequenz des Systems kann zu verfälschten Signalen und Aliaseffekten führen, die unerwünscht und unvermeidbar sind.

PIXELTIEFE/GRAUSKALA

Die Pixeltiefe wird oft auch als "Grauskala" oder (weniger exakt) als Dynamikbereich einer CCD-Kamera bezeichnet und gibt an, wie viele Graustufen es in dem Bild gibt. Die Pixeltiefe hängt eng zusammen mit dem Mindestkontrast, den ein Sensor erkennen kann. Bei Analogkameras ist das Signal eine zeitabhängige Spannung, die proportional zur einfallenden Lichtintensität ist, solange der Sättigungspunkt des Sensors nicht erreicht wird. Nach der Digitalisierung ist diese kontinuierliche Spannung effektiv in diskrete Pegel aufgeteilt, wobei jeder einem numerischen Wert entspricht. Bei einer Gain-Einstellung von 1 erhält ein Pixel, das durch das einfallende Licht zu 100 % gesättigt wird, den Wert 2^N-1, wobei N die als Pixeltiefe spezifizierte Anzahl der Bits ist. Wenn kein Licht auf den Sensor fällt, erhält das Pixel den Wert 0. Techniktipp Nr. 6: Je mehr Bits eine Kamera hat, umso feiner ist die Digitalisierung. Mehr Bits bedeutet außerdem höhere Genauigkeit und mehr Informationen. Wenn genug Bits vorhanden sind, kann das menschliche Auge nicht mehr zwischen einer kontinuierlichen Grauskala und deren digitaler Wiedergabe unterscheiden. Die Anzahl der Bits bei der Digitalisierung ist die sogenannte Pixeltiefe oder Bit-Tiefe.

Ein Beispiel für die Pixeltiefe sind die Kameras der Serie Sony XC mit 256 Graustufen und die Serie der CMOS-Kameras von Edmund Optics für USB 2.0, die mit einer Bit-Tiefe von 8 Bit (256 Graustufen) und 10 Bit (1024 Graustufen) angeboten werden. Allgemein ist es bei Kameras mit einer Bit-Tiefe von 12 oder 14 Bit möglich, die Kamera mit einer geringeren Pixeltiefe zu betreiben. Pixeltiefen von mehr als 8 Bit sind zwar für die Signalverarbeitung vorteilhaft, der Computer zeigt jedoch nur eine Auflösung von 8 Bit an. Wenn die Bilder der Kamera nur auf einem Monitor angezeigt werden, führen die zusätzlichen Daten zu keiner Verbesserung, reduzieren aber die Bildwiederholfrequenz. Abbildung 5 zeigt verschiedene Pixeltiefen. Der Übergang von grau zu weiß ist umso sanfter, je höher die Pixeltiefe ist.

Abb.5: Abbildung verschiedener Grauskalen

DYNAMIKBEREICH

Der Dynamikbereich bezeichnet den Unterschied zwischen der niedrigsten erkennbaren Lichtstärke und der höchsten erkennbaren Lichtstärke. Physikalisch hängt er von der Sättigungskapazität jedes Pixels, dem Dunkelstrom oder Hintergrundrauschen, dem A/D-Wandler und den Gain-Einstellungen ab. Techniktipp Nr. 7: Bei hohen Dynamikbereichen werden mehr Bits benötigt, um diesen sinnvoll auf die Grauskala abzubilden. Umgekehrt ergibt eine Pixeltiefe von 14 Bit, unter Berücksichtigung des Signal-Rausch-Verhältnisses, zur Beschreibung eines Dynamikbereichs von 50 dB redundante Bits und liefert keine zusätzlichen Informationen.

SIGNAL-RAUSCH-VERHÄLTNIS (SNR)

Das Signal-Rausch-Verhältnis (SNR) hängt eng mit dem Dynamikbereich einer Kamera zusammen. Techniktipp Nr. 8: Ein höheres Signal-Rausch-Verhältnis ergibt mehr mögliche Graustufen (höheren Kontrast) für eine Kameraaufnahme. Das Signal-Rausch-Verhältnis wird bei Analogsystemen in Dezibel (dB) und bei Digitalsystemen in Bits angegeben. Allgemein entsprechen 6 dB bei einem analogen Signal-Rausch-Verhältnis einem digitalen Signal-Rausch-Verhältnis von 1 Bit. Bei Digital- bzw. Analogkameras entsprechen X Bits (bzw. dessen Äquivalent bei Analogsystemen) 2^X Graustufen (das heißt z.B., 8-Bit-Kameras haben 2⁸ oder 256 Graustufen).

Das Rauschen in Kamerasensoren wird vor allem durch zwei Quellen verursacht. Die erste Ursache sind Fehler im Chip, die zu einem uneinheitlichen Dunkelstrom und gegenseitigen Störungen führen. Die zweite Quelle ist das Wärmerauschen sowie sonstige Spannungschwankungen. Chipfehler und elektronisches Rauschen reduzieren die Auflösung der Kamera und sollten nach Möglichkeit berücksichtigt und kompensiert werden.

Die Auflösung einer Kamera hängt von so unterschiedlichen Parametern wie der Pixelzahl und der Pixelgröße, den TV-Zeilen, der Kamera-MTF, der Nyquist-Grenzfrequenz, der Pixeltiefe/Grauskala, dem Dynamikbereich und dem Signal-Rausch-Verhältnis ab. Die Kenntnis dieser Begriffe ist der erste Schritt vom Laien zum Experten für Kamerasysteme. Weitere Informationen über die Bildgebungselektronik finden Sie in den restlichen Teilen unserer (zusätzlichen) Serie Bildgebungselektronik 101. Dort werden Kamerasensoren, Kamera-Varianten und Kameraeinstellungen ausführlich behandelt.