Laserresonator und Resonatormoden
Dies ist Abschnitt 4.1 des Leitfadens für Laseroptiken.
In diesem Text erhalten Sie Antworten auf die folgenden Fragestellungen:
- Was ist ein Resonator?
- Welche Laserresonatormoden gibt es?
Was ist ein Resonator?
Die Form eines Laserstrahls wird durch den Resonator bestimmt. Dies ist ein optisches Laserspiegelsystem, in welchem das Laserlicht in einem Verstärkungsmedium verstärkt wird. Laserresonatoren werden normalerweise aus hochreflektierenden dielektrischen Spiegeln oder monolithischen Kristallen, welche die interne Totalreflexion nutzen, um ein Austreten des Lichts zu verhindern, aufgebaut (Abbildung 1). Nachstehend sind einige gebräuchliche Laserresonatorgeometrien aufgelistet1:
- Planparalleler Resonator: zwei flache Spiegel in einem Abstand, der einem ganzzahligen Vielfachen einer halben Laserwellenlänge entspricht
- Konzentrischer Resonator: zwei sphärische Spiegel mit dem gleichen Krümmungsradius und zusammenfallenden Krümmungsmittelpunkten
- Konfokaler Resonator: zwei sphärische Spiegel mit dem gleichen Krümmungsradius und zusammenfallenden Brennpunkten
- Ringresonator: mehr als zwei ringförmig angeordnete Reflektoren, wobei die gesamte geschlossene Weglänge des reflektierten Lichts einem ganzzahligen Vielfachen der halben Laserwellenlänge entspricht
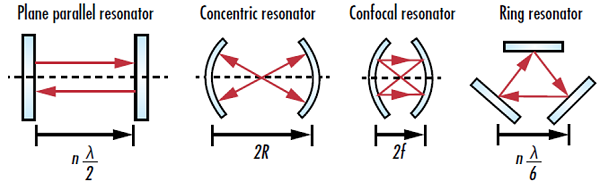
Abbildung 1: Vier gebräuchliche Laserresonatorgeometrien (dabei ist n ein ganzzahliger Wert, λ die Laserwellenlänge, R der Krümmungsradius eines gekrümmten Spiegels und f die Brennweite eines gekrümmten Spiegels).
Resonatorhohlräume sind „stabil“, wenn das reflektierte Licht im Hohlraum bleibt – auch wenn die Anzahl der Reflexionen unendlich groß wird (Abbildung 2). In diesem Fall kann das Licht den Hohlraum nur über einen teilreflektierenden Spiegel verlassen. Demgegenüber werden Resonatorhohlräume als „instabil“ angesehen, wenn das reflektierte Licht laufend divergiert, wenn sich die Anzahl der Reflexionen unendlich nähert. In diesem Fall wird der Strahl immer größer, bis er größer ist als die Reflektoren, und tritt dann aus dem System aus. Stabile Resonatoren werden oftmals bei Lasern mit Leistungen bis 2 kW verwendet, um eine hohe Verstärkung zu erreichen und die Direktionalität zu verbessern. Instabile Resonatoren werden normalerweise bei Lasern mit höheren Leistungen verwendet, um die Wahrscheinlichkeit einer Beschädigung der Reflektoren zu verringern.1

Abbildung 2: Bei stabilen Laserresonatoren bleiben alle reflektierten Strahlen innerhalb der Begrenzungen des Hohlraums, während sich das reflektierte Licht bei instabilen Resonatoren immer mehr ausbreitet, bis es schließlich aus dem Hohlraum austritt.
Die Weglänge des Resonatorhohlraums bestimmt die longitudinalen Resonatormoden oder elektrischen Feldverteilungen, die eine stehende Welle im Hohlraum bewirken. Die Moden eines Strahls legen dessen Form fest. Diese Moden wahren ihr Amplitudenprofil und pflanzen sich selbst nach einer geschlossenen Weglänge im Resonator fort (abgesehen von einem möglichen Leistungsverlust aufgrund von Verlusten im Hohlraum). Damit ein Resonanzzustand entsteht, muss in einer geschlossenen Weglänge eine Phasenverschiebung erfolgen, die einem ganzzahligen Vielfachen von 2π entspricht (Abbildung 3).
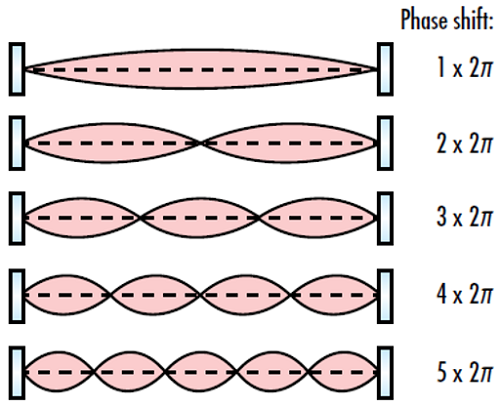
Abbildung 3: Die Phasenverschiebung einer vollständigen Weglänge in einem optischen Resonator muss ein ganzzahliges Vielfaches von 2π sein, damit ein Resonanzzustand entsteht.
Welche Laserresonatormoden gibt es?
Die einfachsten Laserresonatormoden sind Hermite-Gauß-Moden, die auch transversale elektromagnetische Moden (TEMnm) genannt werden, in denen das elektrische Feldprofil durch das Produkt einer Gauß-Funktion mit einem Hermite-Polynom angenähert werden kann2:
E_{nm} \! \left(x, y, z \right) = & \, E_0 \frac{w_0}{w \! \left( z \right)} \, \cdot \, H_{n} \left( \sqrt{2} \frac{x}{w \! \left( z \right)} \right) \\
& \cdot \exp{\left( -\frac{x^2}{w \! \left( z \right) ^2} \right)} \, \cdot \, H_m \left( \sqrt{2} \frac{y}{w \! \left( z \right)} \right) \cdot \exp{\left( -\frac{y^2}{w \! \left( z \right) ^2} \right)} \\
& \cdot \, \exp{\Bigg[ -i \left[ kz - \left( 1 + n + m \right) \cdot \tan^{-1}{\left( \frac{z}{z_R} \right)} + \frac{k \left( x^2 + y^2 \right)}{2 R \! \left( z \right) } \right] \Bigg]}
\end{align}
oder
- E0 ist das Feldmaximum
- x und y sind die Achsen, die den Querschnitt des Strahls definieren
- z ist die Ausbreitungsachse
- w0 ist die Strahltaille
- w(z) ist der Strahlradius bei einem gegebenen z-Wert
- Hn(x) und Hm(x) sind die Hermite-Polynome mit den nicht-negativen ganzzahligen Indizes n und m
- k ist die Wellenzahl (k=2π/λ)
- zR ist die Rayleighlänge
- R(z) ist der Krümmungsradius der Wellenfront
Die Ganzzahlen n und m definieren die Strahlform in x- bzw. y-Richtung. Ein idealer gaußscher Strahl wird durch die Mode TEM00 definiert, bei der sowohl n als auch m gleich 0 sind (Abbildung 4). Weitere Informationen zu gaußschen Strahlen finden Sie in unserem Anwendungshinweis zur Ausbreitung gaußscher Strahlen. Bei allen anderen Werten von n und m entstehen komplexere Resonatormoden.3 In Abbildung 5 sind die Querschnittsgeometrien der Hermite-Gauß-Moden niedrigster Ordnung mit Werten für n und m von 0 bis 3 dargestellt.

Abbildung 4: Die Hermite-Gauß-Resonatormode TEM00 entspricht einem idealen gaußschen Strahl.

Abbildung 5: Querschnitte der Hermite-Gauß-Resonatormoden niedrigster Ordnung mit Werten für n und m von 0 bis 3.
Referenzen
- “Section 2.6: Various Laser Resonators.” Advanced Manufacturing Laboratory, Columbia Engineering, www.aml.engineering.columbia.edu/ntm/level2/ch02/html/l2c02s06.html.
- Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
- Paschotta Rüdiger. Field Guide to Lasers. SPIE Press, 2008.
More Resources













 Vorheriger Abschnitt
Vorheriger Abschnitt 













weitere regionale Telefonnummern
ANGEBOTSTOOL
Geben Sie zum Starten die Produktnummer ein.
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
DATENSCHUTZRICHTLINIE | COOKIE POLICY | AGB | AGB FÜR B2C | IMPRESSUM | BARRIEREFREIHEIT
Die Edmund Optics GmbH Deutschland fungiert als Handelsvermittler für die Edmund Optics BV in den Niederlanden.
Vertragspartner ist Edmund Optics BV in den Niederlanden.
The FUTURE Depends On Optics®