Strahlqualität eines Lasers und Strehl-Verhältnis

Um die tatsächliche qualitative Leistung eines Lasers genau vorherzusagen, muss der M²-Faktor des Lasers bekannt sein, der die Qualität des Strahls beschreibt. Wenn die Leistung eines Lasers bekannt ist, kann über die tatsächliche Leistung eines optischen Systems, das mit dem Laser verwendet wird, die endgültige Systemleistung ermittelt werden. Der Vergleich der tatsächlichen Leistung eines optischen Systems mit der idealen, beugungsbegrenzten Leistung erfolgt über das Strehl-Verhältnis. 

M²-Faktor

Die Strahlqualität eines Lasers wird durch den M²-Faktor (Beugungsmaßzahl) charakterisiert, der die tatsächliche Form des Strahls mit der Form eines idealen gaußschen Strahls vergleicht. Die ISO-Norm 11146 definiert den M²-Faktor wie folgt¹:

In Gleichung 1 ist w₀ die Strahltaille, θ ist der Divergenzwinkel des Lasers und λ ist die Laserwellenlänge (Abbildung 1). Wie in unserem Anwendungshinweis zur Ausbreitung gaußscher Strahlen beschrieben, wird der Divergenzwinkel eines gaußschen Strahls durch folgende Gleichung bestimmt:

Durch Einsetzen des ermittelten Divergenzwinkels in Gleichung 1 wird die Gleichung für den M²-Faktor eines gaußschen Strahls wie folgt vereinfacht:

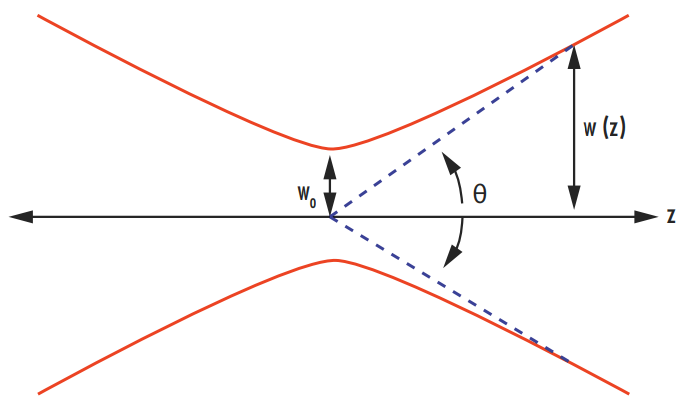
Abbildung 1: Veranschaulichung von Divergenzwinkel und Strahltaille eines Laserstrahls.

Ein M²-Faktor entspricht somit einem beugungsbegrenzten gaußschen Strahl. Bei größeren M²-Faktoren (> 1) weicht der Strahl von einem idealen gaußschen Strahl ab. Ein Wert kleiner 1 kann nicht erreicht werden. Der M²-Faktor einer Hermite-Gauß-Mode beträgt (2n + 1) in x-Richtung und (2m + 1) in y-Richtung.² Die Mode TEM₁₃ weist beispielsweise einen M²-Faktor von 3 in x-Richtung und von 7 in y-Richtung auf. Ein normaler Helium-Neon-Laser verfügt über einen M²-Faktor zwischen 1 und 1,1. Weitere Informationen zu Hermite-Gauß-Moden finden Sie in unserem Anwendungshinweis zu Laserresonatormoden.

Zusammen mit der optischen (energetischen) Leistung eines Laserstrahls bestimmt der M²-Faktor die Strahldichte (Radianz) des Strahls. Der M²-Faktor kann auch für die Approximation des Radius eines Strahls bei der Ausbreitung verwendet werden, indem die Wellenlänge eines Lasers in allen Gleichungen im Anwendungshinweis zur Ausbreitung gaußscher Strahlen durch die Wellenlänge multipliziert mit dem M²-Faktor ersetzt wird.³

Der M²-Faktor ist eine wichtige Kenngröße, da er beschreibt, wie gut ein Laserstrahl bei einer gegebenen Divergenz fokussiert werden kann. Kleinere M²-Faktoren entsprechen einem engeren Fokus, einer effektiveren Nutzung der Leistung im Strahl und einer höheren möglichen Wirkleistung des Lasers.

Die Messung des M²-Faktors ist schwieriger als die Messung des Strahlprofils auf einer einzelnen Ebene der Laserachse. ISO 11146 schreibt vor, dass fünf Strahlradiusmessungen an verschiedenen Positionen auf der optischen Achse im Nahfeld und im Fernfeld gemessen werden müssen.⁴ Es ist möglich, dass ein Strahl in einer bestimmten Ebene wie ein idealer gaußscher Strahl aussieht, ohne dass überhaupt eine TEM₀₀-Mode enthalten ist (Abbildung 2). Obwohl der Querschnitt auf der betreffenden Ebene wie eine perfekte gaußsche Verteilung aussieht, breitet sich der Strahl vollkommen anders aus als ein gaußscher Strahl, und der Divergenzwinkel des Strahls ist größer.⁵ Mehrere Radiusmessungen auf verschiedenen Ebenen lassen schnell den Unterschied zwischen diesem Strahl und einem echten gaußschen Strahl erkennen. Der gemessene Strahlradius (w(z)) hängt wie folgt von der Strahltaille (w₀)der Wellenlänge (λ) und dem M²-Faktor ab:⁶ 

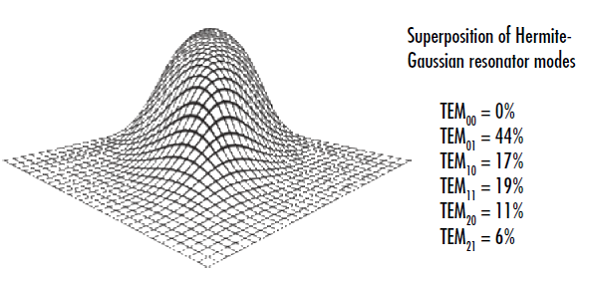
Abbildung 2: Dieser Strahlquerschnitt sieht auf einer bestimmten Ebene wie ein gaußscher Strahl aus, obwohl er keine TEM₀₀-Mode enthält, und verdeutlicht die Notwendigkeit mehrerer Intensitätsmessungen entlang der Laserachse, um den M₂-Faktor eines Lasers zu bestimmen.

Ein Nachteil der Charakterisierung von Strahlen mit dem M2-Faktor im Vergleich zu anderen Strahlqualitätsparametern besteht darin, dass die „Flügel“ (d. h. die Teile des Strahls mit geringerer Leistungsdichte weit weg vom Mittelpunkt) stärker betont werden, sodass er bisweilen besser für wissenschaftliche Laborumgebungen geeignet ist als für industrielle Anwendungen.

Strahlparameterprodukt

Das Strahlparameterprodukt (SPP) ist eine weitere Kenngröße für die Bewertung der Qualität eines Laserstrahls. Es ist als Produkt des Strahlradius an der Strahltaille und dem halben Winkel der Strahldivergenz definiert. Es wird normalerweise in [mm mrad] angegeben und hängt wie folgt vom M²-Faktor ab:

Da das SPP direkt proportional zum M²-Faktor ist, entspricht ein größeres Strahlparameterprodukt einem Strahl von geringerer Qualität. Der kleinste SPP-Wert ist λ/π und ist nur bei einem idealen gaußschen Strahl möglich.

Das SPP wird häufig für die Charakterisierung von Faserlasern oder Halbleiterlasern mit großen M²-Faktoren sowie für Diodenlasersysteme mit Faserankopplung verwendet, um die Lichtmenge zu bestimmen, die in einen Lichtleiter eingekoppelt werden kann.

Power-in-the-Bucket

Power-in-the-Bucket (PIB) ist eine weitere Kenngröße zur Definition der Strahlqualität und wird häufig in Hochleistungslasersystemen und Materialbearbeitungsanwendungen verwendet. PIB beschreibt, wie groß das Integral der Laserleistung in einem bestimmten „Bucket“ ist. Dabei handelt es sich meistens um eine Stelle mit einem bestimmten Radius auf der bearbeiteten Materialoberfläche. Obwohl dieses Konzept scheinbar einfach ist, muss die Bucketform im Fernfeld klar definiert sein. Außerdem hängen Vergleiche mit idealen Szenarien von der Spezifikation der idealen Laserstrahlform im Nahfeld ab.
Da es keinen Industriestandard für die exakte PIB-Definition gibt, wird diese Kenngröße oftmals als vertikale oder horizontale Strahlqualität angegeben:⁷

Genauso wie beim M²-Faktor und SPP entspricht ein kleinerer PIB-Wert einem Strahl höherer Qualität. Der PIB-Wert kann grafisch als Anteil der Leistung im definierten „Bucket“ als Funktion von λ/D dargestellt werden, wobei D der Durchmesser des Nahfeldstrahls ist (Abbildung 3). Die vertikale Strahlqualität ist die Quadratwurzel des Verhältnisses vom Leistungsanteil im Bucket eines idealen gaußschen Strahls zum Leistungsanteil im Bucket des tatsächlichen Strahls bei einem gegebenen λ/D (entsprechend der vertikalen Abmessung im Diagramm). Die horizontale Strahlqualität ist das Verhältnis vom λ/D-Wert eines idealen gaußschen Strahls zum λ/D-Wert des tatsächlichen Strahls bei einem gegebenen Leistungsanteil im Bucket (entsprechend der horizontalen Abmessung im Diagramm).

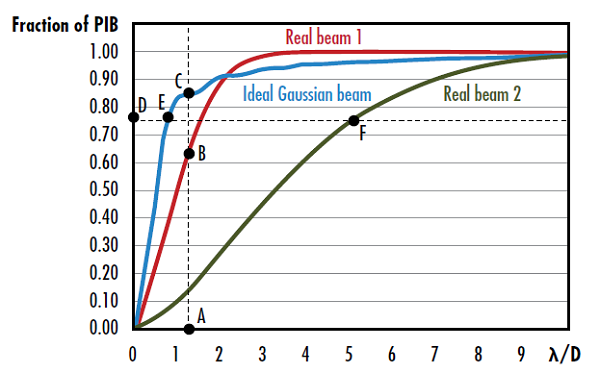
Abbildung 3: Die vertikale Strahlqualität des Strahls 1 ist die Quadratwurzel des Verhältnisses des Segments AC zum Segment AB. Die horizontale Strahlqualität des Strahls 2 ist das Verhältnis des Segments DF zum Segment DE.⁷

Kreisförmige und elliptische Strahlen

Bei der Betrachtung der Form eines Laserstrahls ist die Bestimmung, ob der Laser einen kreisförmigen oder einen elliptischen Strahl erzeugt, von Bedeutung. Elliptische Strahlen können nachteilig für die Systemleistung sein, da sie im Vergleich zu kreisförmigen Strahlen eine größere fokussierte Spotgröße aufweisen. Diese größere Spotgröße führt zu einer geringeren Strahlungsintensität (Strahlungsenergiefluss pro Flächeneinheit) als bei einem kreisförmigen Strahl, sodass u. U. eine höhere Eingangsleistung für den Laser notwendig ist. Halbleiterlaserdioden emittieren elliptisch geformte Strahlen mit unterschiedlichen Divergenzwinkeln in x- und y-Richtung aufgrund der rechteckigen Form der aktiven Region (Abbildung 4). Die Beugung ist bei kleinen Aperturen größer, sodass kleinere Abmessungen der aktiven Region einen Strahl mit höherer Divergenz erzeugen und ein astigmatischer Strahl entsteht. Die Achse mit dem größeren Divergenzwinkel wird schnelle Achse genannt, die Achse mit dem kleineren Divergenzwinkel langsame Achse. Um elliptische Strahlen kreisförmig zu machen, werden oftmals Zylinderlinsen verwendet (Abbildung 5). Weitere Informationen zu Zylinderlinsen finden Sie in unserem Anwendungshinweis mit Überlegungen zur Verwendung von Zylinderlinsen.

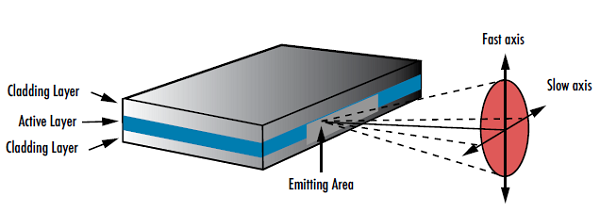
Abbildung 4: Die Geometrie von Laserdioden bewirkt, dass elliptische Strahlen mit zwei verschiedenen Divergenzwinkeln entstehen.

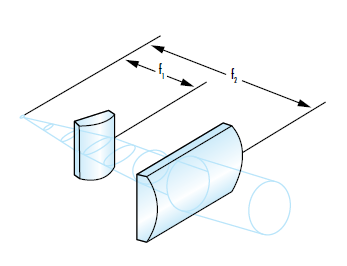
Abbildung 5: Um elliptische Strahlen kreisförmig zu machen, werden oftmals Zylinderlinsen verwendet, die die schnelle und die langsame Achse unterschiedlich beeinflussen.

Strehl-Verhältnis

Genauso wie der M²-Faktor die tatsächliche Leistung eines Lasers mit der eines idealen Strahls vergleicht, vergleicht das Strehl-Verhältnis von optischen Systemen oder Komponenten die tatsächliche Leistung mit einer idealen Version. Das Strehl-Verhältnis von Fokussieroptiken, wie z. B. sphärischen und asphärischen Linsen, ist das Verhältnis der maximalen Strahlungsintensität im Brennfleck der tatsächlichen Optik ausgehend von einer Punktquelle zur idealen maximalen Beleuchtungsstärke einer theoretischen beugungsbegrenzten Optik (Abbildung 6).⁷ Ein Strehl-Verhältnis von 1 gibt an, dass eine Optik perfekt und aberrationsfrei ist. In der industriellen Praxis wird eine Linse als „beugungsbegrenzt“ betrachtet, wenn das Strehl-Verhältnis größer als 0,8 ist.

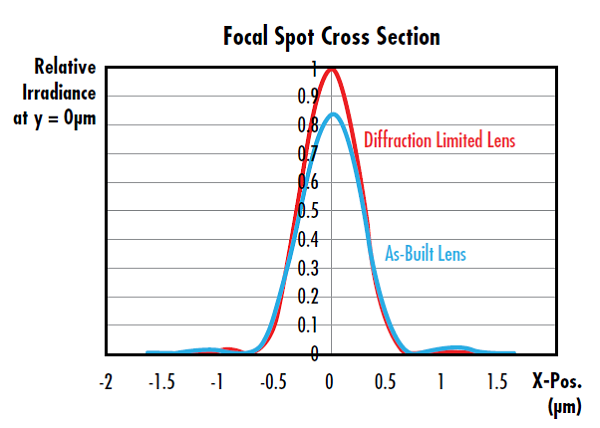
Abbildung 6: Diese Linse weist ein Strehl-Verhältnis von 0,826 auf und wird als beugungsbegrenzt betrachtet, weil das Verhältnis größer als 0,8 ist.

Das Strehl-Verhältnis einer Optik hängt näherungsweise vom RMS-Wert des transmittierten Wellenfrontfehlers ab Gleichung 8 Dabei ist S das Strehl-Verhältnis und σ ist der RMS-Wert des Wellenfrontfehlers in Wellen der Optik.⁸ Diese Näherung ist zulässig, wenn der Wellenfrontfehler kleiner als 0,2 Wellen ist.

Weitere Informationen zum Einfluss des Passfehlers einer Oberfläche auf das jeweilige Strehl-Verhältnis finden Sie in unserem Anwendungshinweis Passfehler asphärischer Linsen und Strehl-Verhältnis.

Referenzen

1. International Organization for Standardization. (2005). Lasers and laser-related equipment – Test methods for laser beam widths, divergence angles and beam propagation ratios (ISO 11146).
2. A. E. Siegman, “New developments in laser resonators”, Proc. SPIE 1224, 2 (1990)
3. Paschotta, Rüdiger. Encyclopedia of Laser Physics and Technology, RP Photonics, October 2017, www.rp-photonics.com/encyclopedia.html.
4. International Organization for Standardization. (2005). Lasers and laser-related equipment — Test methods for laser beam widths, divergence angles and beam propagation ratios — Part 1: Stigmatic and simple astigmatic beams (ISO 11146-1:2005).
5. A. Siegman, “’Non-Gaussian’ Beam”, OSA Annual Meeting, Long Beach, CA (1997)
6. Hofer, Lucas. “M² Measurement.” DataRay Inc., 12 Apr. 2016, www.dataray.com/blog-m2-measurement.html.
7. Strehl, Karl W. A. “Theory of the telescope due to the diffraction of light,” Leipzig, 1894.
8. Mahajan, Virendra N. "Strehl ratio for primary aberrations in terms of their aberration variance." JOSA 73.6 (1983): 860-861.

Vorheriger Abschnitt Nächster Abschnitt