Passfehler asphärischer Linsen und Strehl-Zahl
Dies sind die Abschnitte 7.1 und 7.2 des Leitfadens für Laseroptiken.
Alle optischen Systeme verfügen über eine theoretische Leistungsgrenze, die sogenannte Beugungsgrenze. Das Strehl-Verhältnis – oder auch die Strehl-Zahl – ist eine Spezifikation zum Vergleich der tatsächlichen Leistung eines optischen Systems mit seiner entsprechenden beugungsbegrenzten Leistung. Für asphärische Linsen und andere Fokussieroptiken ist die Strehl-Zahl definiert als das Verhältnis der beobachteten maximalen Strahlungsintensität im Brennfleck einer gefertigten Optik zur theoretischen beugungsbegrenzten maximalen Strahlungsintensität (Abbildung 1).1 Die verschiedenen Fertigungsverfahren für asphärische Linsen verursachen spezifische Oberflächenfehler, die sich unterschiedlich auf die Strehl-Zahl auswirken. Für die korrekte Spezifikation von Asphären müssen diese Effekte berücksichtigt werden, um unnötige und kostspielige Überspezifikationen zu vermeiden, die gewünschten Spezifikationen aber zu erfüllen. Dies wird zunehmend für Asphären mit kleinen Blendenzahlen (f/#) von Bedeutung und gilt insbesondere für Asphären, die mit herkömmlichen Schleif- und Polierverfahren gefertigt werden (andere Verfahren sind weniger betroffen). Der branchenübliche Schwellenwert, ab dem eine Linse als „beugungsbegrenzt“ klassifiziert wird, ist eine Strehl-Zahl größer 0,8.

Abbildung 1: Querschnitt der Strahlungsintensität durch den Brennfleck einer asphärischen f/2-Linse mit einem Durchmesser von 25 mm bei 588 nm Die Strehl-Zahl der gefertigten Linse ist 0,826 und erfüllt damit das Kriterium für beugungsbegrenzte Optiken
Die Strehl-Zahl kann auch mit dem RMS-Wert des transmittierten Wellenfrontfehlers ins Verhältnis gesetzt werden. Dazu wird die folgende Näherungsformel verwendet, wobei $ \small{\sigma} $ der RMS-Wellenfrontfehler angegeben in Wellen ist.2 Diese Annäherung gilt für Wellenlängen mit transmittierten Wellenfrontfehlern <0.2.3
Auswirkung des Passfehlers der Oberfläche auf die Strehl-Zahl
Die Strehl-Zahl einer Optik hängt stark vom Passfehler ihrer Oberfläche ab – also davon, inwieweit die optische Oberfläche von der Nennform abweicht. Der Passfehler der Oberfläche variiert je nach verwendetem Fertigungsverfahren. Sphärische Optiken werden gewöhnlich mit einem überdimensionierten Werkzeug poliert, das geringe räumliche Frequenzfehler auf der optischen Oberfläche verursacht. Bei der Herstellung von Asphären wird dagegen typischerweise Subapertur-Schleifen und -Polieren eingesetzt, was komplexere strukturierte Unregelmäßigkeiten hinterlässt. Das Verständnis der Beziehung zwischen dem spezifizierten Passfehler einer Oberfläche und der zugrundeliegenden Struktur kann Einblick in die Leistung der Linse und die sich daraus ergebende Strehl-Zahl bieten.
Betrachten Sie zum Beispiel die Auswirkungen der Raumfrequenz. Wenn der Passfehler einer Oberfläche als rotationssymmetrische Kosinusfunktion modelliert wird, können wir die resultierende Strehl-Zahl als Funktion des RMS-Passfehlers einer Oberfläche für verschiedene Kosinusperioden untersuchen (Abbildung 2 und Abbildung 3).
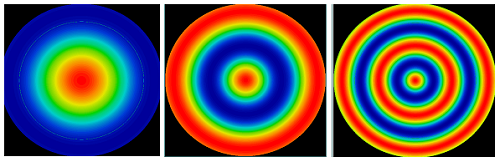
Abbildung 2: Typische Passfehler einer Oberfläche bei der Fertigung von asphärischen Linsen folgen – wie bei diesen Karten für einen radialen kosinusförmigen Passfehler auf einer f/2-Asphärenoberfläche mit einem Durchmesser von 25 mm – einem Kosinusmuster. Die Kosinusperioden von links nach rechts betragen 20 mm, 10 mm und 5 mm.

Abbildung 3: Je mehr Kosinusperioden bei einem bestimmten RMS-Passfehler einer Oberfläche in der Apertur der Asphäre vorhanden sind, desto kleiner ist die Strehl-Zahl.
Der hier entscheidende Faktor ist nicht die Kosinusperiode in mm, sondern die Anzahl der Perioden in der Apertur der Linse. Für ein bestimmtes Subaperturwerkzeug, das in der Asphärenfertigung eingesetzt wird, weisen Asphären mit einem kleineren Durchmesser eine geringere Verschlechterung der Strehl-Zahl auf als Asphären mit einem größeren Durchmesser.
Die Auswirkung des Passfehlers der Oberfläche auf die Strehl-Zahl hängt auch von der Blendenzahl (f/#) der Linse ab. Allgemein gilt, dass sich der Passfehler der Oberfläche bei schnelleren Asphären, d. h. Asphären mit kleineren Blendenzahlen, stärker auf die Strehl-Zahl auswirkt. Abbildung 4 vergleicht beispielsweise eine f/2-Linse mit einer f/0,75-Linse (beide mit einem Durchmesser von 25 mm). Die Verschlechterung der Strehl-Zahl ist bei schnelleren Linsen im Vergleich zu langsameren Linsen bei einer bestimmten Kosinusperiode größer.
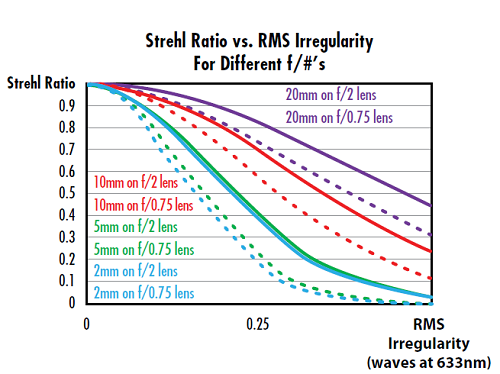
Abbildung 4: Der Vergleich der gepunkteten Linien mit den durchgezogenen Linien zeigt, dass eine schnellere Asphäre (kleinere Blendenzahl f/#) bei einer bestimmten Kosinusperiode eine größere Verschlechterung aufweist als eine langsamere Asphäre (größere Blendenzahl f/#).
Spektrale Leistungsdichte und Passfehlersteigung
Die obigen Beispiele zeigen deutlich, dass sich der Raumfrequenzinhalt der Passfehlerkarten auf die Strehl-Zahl der Linse auswirkt. Zusätzlich zum PV- (Peak to Valley) oder RMS-Wert des Passfehlers können weitere Spezifikationen für diese Raumfrequenzen angefordert werden.
Eine Spezifikation, die für die direkte Auswertung der Raumfrequenzen verwendet werden kann, ist die spektrale Leistungsdichte (SLD).4 Die SLD wertet den Passfehler einer Oberfläche als Funktion der Raumfrequenz aus und bietet die Möglichkeit, den Beitrag bestimmter Raumfrequenzen gezielt zu begrenzen. Die SLD kann auch verwendet werden, um alle Raumfrequenzen gleichzeitig zu beschränken.
Eine einfache und gleichzeitig effektive Methode zum Reduzieren höherer Raumfrequenzen im Passfehler besteht darin, zusätzlich zum PV-Wert die Steigung der Kosinusfunktionen der Oberflächenpassfehlerkarte zu beschränken. Für einen bestimmten PV-Passfehlergrenzwert führen größere Steigungen zu höheren Raumfrequenzen auf der Oberfläche (Abbildung 5). Die Steigung wird oftmals als maximaler RMS-Steigungswert angegeben. Dieser ermöglicht eine umfassendere Bewertung der Linsenoberfläche als lediglich eine gewünschte maximale Steigung.5
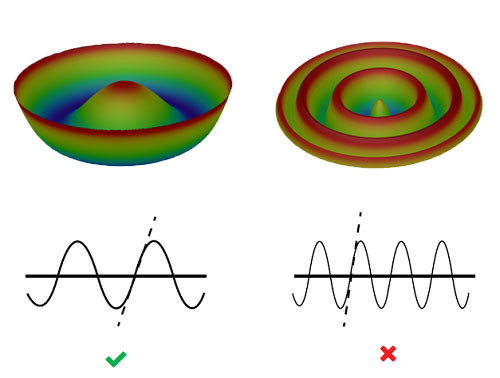
Abbildung 5: Die Spezifikation einer maximalen Steigung für die Oberflächenpassfehlerkarte definiert einen Schwellenwert, um die Auswirkung des Inhalts höherer Raumfrequenzen auf der Oberfläche zu reduzieren.
Die Raumfrequenz des Passfehlers einer Oberfläche wirkt sich erheblich auf die Strehl-Zahl und die Asphärenleistung aus. Je kleiner die Periode ist, desto größer ist die Verschlechterung der Strehl-Zahl bei einem gegebenen Passfehler der Oberfläche. Die Form der Oberflächenpassfehlerkarte einer Linse muss bekannt sein, um die wahre Auswirkung des Passfehlers der Oberfläche auf die Leistung der Linse zu verstehen. Eine Passfehlerspezifikation allein reicht nicht aus.6 Kleinere Blendenzahlen führen ebenfalls zu einer größeren Verschlechterung.
Referenzen
- Strehl, Karl W. A. “Theory of the telescope due to the diffraction of light,” Leipzig, 1894.
- Mahajan, Virendra N. "Strehl ratio for primary aberrations in terms of their aberration variance." JOSA 73.6 (1983): 860-861.
- Smith, Warren J. Modern Optical Engineering. 4th ed., McGraw-Hill Education, 2007.
- Lawson, Janice K., et al. "Specification of optical components using the power spectral density function." Optical Manufacturing and Testing. Vol. 2536. International Society for Optics and Photonics, 1995.
- Messelink, Wilhelmus A., et al., "Mid-spatial frequency errors of mass-produced aspheres," Proc. SPIE 10829, Fifth European Seminar on Precision Optics Manufacturing, 7 Aug. 2018, doi:10.1117/12.2318663.
- Kasunic, Keith J., Laser Systems Engineering, SPIE Press, 2016. (ISBN 9781510604278)













 Vorheriger Abschnitt
Vorheriger Abschnitt 








































weitere regionale Telefonnummern
ANGEBOTSTOOL
Geben Sie zum Starten die Produktnummer ein.
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
Die Edmund Optics GmbH Deutschland fungiert als Handelsvermittler für die Edmund Optics Ltd. in Großbritannien.
Vertragspartner ist die Edmund Optics Ltd. in Großbritannien.