Alles über Asphären
Zum Einstieg: Die Vorteile einer Asphäre

Korrektur des Öffnungsfehlers
Der große Vorteil von Asphären ist ihre Fähigkeit, die sphärische Aberration zu korrigieren. Dieser Abbildungsfehler ergibt sich, wenn eine sphärische Form zur Fokussierung oder Kollimierung von Licht verwendet wird. Mit anderen Worten, alle sphärischen Optiken verursachen sphärische Aberrationen, unabhängig davon, ob Ausrichtungs- oder Fertigungsfehler vorhanden sind. Nur mit einer asphärischen Optik, können diese Fehler vermieden werden. Durch Anpassung der konischen Konstanten und der asphärischen Parameter, kann die Linse so optimiert werden, dass praktisch keine sphärische Aberration mehr auftritt. Abbildung 2 zeigt die Auswirkungen der sphärischen Aberration bei einer gewöhnlichen Linse und verdeutlicht die Vorteile einer Asphäre. Bei einer sphärischen Linse werden einfallende Lichtstrahlen, abhängig von ihrer radialen Position, an verschiedenen Punkten fokussiert. Dadurch entsteht eine Unschärfe in der Abbildung. Die Asphäre fokussiert alle Strahlen auf denselben Punkt, unabhängig von ihrem Auftreffpunkt, was die Abbildung deutlich verbessert.
Eine bessere Vorstellung von der unterschiedlichen Fokussierung einer Asphäre und einer sphärischen Linse bekommen Sie mit Hilfe der folgenden Tabelle. In dem quantitativen Beispiel wurden zwei vergleichbaren Linsen mit 25 mm Durchmesser und einer Brennweite von 25 mm (Linsen f/1) verwendet. Aufgelistet sind die entstehenden Fokusgrößen auf der Achse (Objektwinkel 0°) und außerhalb der Achse (Objektwinkel 0,5° und 1,0°) für kollimierte, monochromatische Lichtstrahlen mit der Wellenlänge 587,6 nm. Da eine bessere Fokussierung ein Hinweis auf bessere optische Eigenschaften im Allgemeinen ist, wird deutlich, wie groß der Vorteil der Asphäre tatsächlich ist. Der Punkt ist um zwei Größenordnungen kleiner, was eine deutlich besser Abbildungsqualität bedeutet.
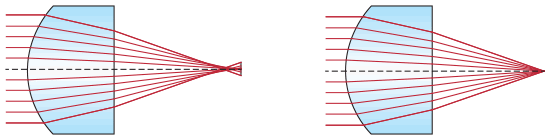
Abbildung 1: Sphärische Aberration (links) einer sphärischen Linse im Vergleich mit einer Asphäre ohne diesen Abbildungsfehler (rechts)
| Objektwinkel (°) | 0,0 | 0,5 | 1,0 |
| Fokusgröße sphärische Linse (μm) | 710,01 | 710,96 | 713,84 |
| Fokusgröße Asphäre (μm) | 1,43 | 3,91 | 8,11 |
Zusätzliche Vorteile
Es gibt zwar verschiedene Verfahren, um sphärische Aberrationen zu korrigieren, keine erreicht jedoch die Abbildungseigenschaften und die Flexibilität von Asphären. Eine höhere Blendenzahl f/#, durch Abblenden der Linse oder einfach durch eine kleinere Linse, verbessert die Abbildungsqualität zwar ebenfalls, allerdings sinkt damit auch der Lichtdurchsatz im System, so dass ein Kompromiss gefunden werden muss.
Bei Einsatz von Asphären erlaubt die inhärente Korrektur der sphärischen Aberration die Konstruktion von Systemen mit hohem Lichtdurchsatz (kleine Blendenzahl f/#, hohe numerische Apertur), bei gleichzeitig guter Bildqualität. Die Abbildungsleistung lässt bei größerer Apertur zwar auch hier nach, die Verluste sind im Vergleich zu sphärischen Systemen allerdings minimal. Das Beispiel zeigt ein dreilinsiges System mit einer Brennweite von 81,5 mm und der Blendenöffnung f/2 (Abb.3), bei der alle Oberflächen sphärisch sind, und das gleiche System mit einer asphärischen Oberfläche. Bei beiden Systemen wurden die gleichen Glassorten, die gleiche effektive Brennweite, das gleiche Bildfeld, die gleiche Blendenöffnung f/# und die gleiche Gesamtlänge verwendet. In der folgenden Tabelle finden Sie einen quantitativen Vergleich der Modulationstransferfunktion (MTF) bei 20 % Kontrast für auf der Achse und außerhalb der Achse einfallendes, kollimiertes, polychromatisches Licht mit den Wellenlängen 486,1 nm, 587,6 nm und 656,3 nm. Das Linsensystem mit der Asphäre hat bei allen Bildwinkeln deutlich bessere Abbildungseigenschaften. Zu erkennen ist das an den hohen meridionalen und sagitalen Auflösungswerten, die um einen Faktor vier besser sind, als bei dem rein sphärischen System.
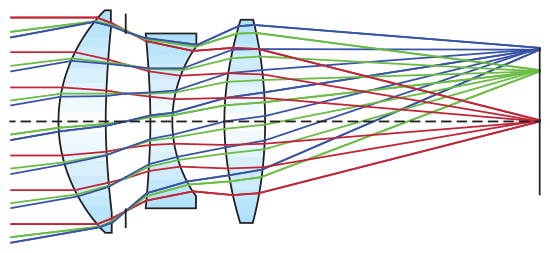
Abbildung 2: Polychromatisches Licht durch ein dreilinsiges System
| Objektwinkel (°) | alle Flächen sphärisch | erste Fläche asphärisch | ||
|---|---|---|---|---|
| Meridional (lp/mm) | Sagittal (lp/mm) | Meridional (lp/mm) | Sagittal (lp/mm) | |
| 0,0 | 13,3 | 13,3 | 61,9 | 61,9 |
| 7,0 | 14,9 | 13,1 | 31,1 | 40,9 |
| 10,0 | 17,3 | 14,8 | 36,3 | 41,5 |
Vorteile des Systems
Mit asphärischen Linsen können Optikdesigner bestimmte Aberrationen mit weniger Elementen korrigieren, als bei konventionellen sphärischen Optiken. Selbst wenn viele Elemente verwendet werden, um mit schwächer gekrümmten Linsen auszukommen, bleibt das geometrische Problem der sphärischen Oberflächen bestehen. Nur Asphären lösen dieses Problem tatsächlich. In Zoomobjektiven werden beispielsweise oft zehn oder mehr Linsenelemente eingesetzt. Dort können ein oder zwei asphärische Linsen, bei vergleichbarer oder besserer Bildqualität, diverse sphärische Linsen ersetzen und damit gleichzeitig die Fertigungskosten minimieren, sowie die Systemgröße reduzieren.
Ein optisches System mit mehr Elementen kann sowohl die optischen als auch die mechanischen Parameter verschlechtern. Es erfordert engere mechanische Toleranzen, zusätzliche Justagearbeiten, und stellt höhere Anforderungen an die Antireflexionsbeschichtung. All diese Faktoren treiben die Kosten nach oben. Daher können durch die Verwendung von Asphären die Gesamtkosten reduziert werden, obwohl diese teurer sind als sphärische Optiken mit denselben Eckdaten.
Anatomie einer Asphäre
Eine asphärische Linse, auch bezeichnet als "Asphäre", ist eine rotationssymmetrische Optik, deren Krümmungsradius sich radial mit dem Abstand vom Mittelpunkt ändert. Sie hat eine höhere Bildqualität, reduziert die Anzahl der benötigten optischen Elemente und senkt die Kosten für bestimmte optische Systeme deutlich. In Digitalkameras und CD-Playern, in High-End-Mikroskopobjektiven und Fluoreszenzmikroskopen finden sich Asphären genauso wie in anderen Bereichen der Optik, der Bildgebung und der Photonik, da sie gegenüber traditionellen sphärischen Optiken deutliche Vorteile haben.
Asphären werden traditionell durch ihr Oberflächenprofil (sag) nach Gleichung 1 definiert:
Hierbei ist:
Z = Sagittalschnitt parallel zur optischen Achse
s = radialer Abstand zur optischen Achse
C = Krümmung, Kehrwert des Radius
k = konische Konstante
A4, A6, A8...= Asphärenkoeffizienten 4., 6., 8. Ordnung
Wenn alle Asphärenkoeffizienten gleich null sind, ergibt sich ein Kegelschnitt. Die folgende Tabelle zeigt, wie die erzeugten Flächen von Größe und Vorzeichen der konischen Konstante k abhängen.
| Konische Konstante | Art der Fläche | |
|---|---|---|
| k = 0 | Sphäre |  |
| k > -1 | Ellipsoid |  |
| k = -1 | Paraboloid |  |
| k < -1 | Hyperboloid |  |
Die typische geometrische Eigenschaft von Asphären ist, dass sich ihr Krümmungsradius mit dem Abstand von der optischen Achse ändert, im Gegensatz zu einer Sphäre, die einen konstanten Radius hat (Abb.1). Durch diese typische Form haben Asphären bessere optische Eigenschaften als Standardlinsen mit sphärischen Oberflächen.
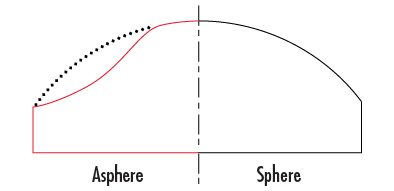
Abbildung 3: Vergleich von sphärischen und asphärischen Oberflächenprofilen
Over the past few years, two other definitions that use orthogonal terms have gained in popularity called Q-type aspheres. These Q-type aspheres, Qcon and Qbfs allow designers more control over the optimization of the aspheres by using orthogonal coefficients and generally reduce the terms needed for manufacturing the asphere.
Wie werden sie hergestellt? Verschiedene Arten von Asphären.
Blankpressen von Glas
Blankpressen von Glas ist ein Fertigungsverfahren, bei dem bestimmte Gläser so lange erhitzt werden, bis die Oberfläche so formbar wird, dass sie in eine asphärische Form gepresst werden kann (Abb.4). Nach Abkühlung der Presslinge bis auf Raumtemperatur, behalten sie die Form des Werkzeugs. Die Fertigung der Pressform bedeutet hohe Anfangskosten, weil sie aus einem sehr haltbaren Material exakt gefertigt werden muss, das zugleich eine glatte Oberfläche behält. Zudem muss die Schrumpfung der Presslinge berücksichtigt werden, um die gewünschte Asphärenform zu erhalten. Wenn die Form jedoch einmal vorhanden ist, sind die Folgekosten pro Linse niedriger als bei den Standardfertigungsverfahren, so dass sich hier eine großartige Möglichkeit für die Massenproduktion ergibt.
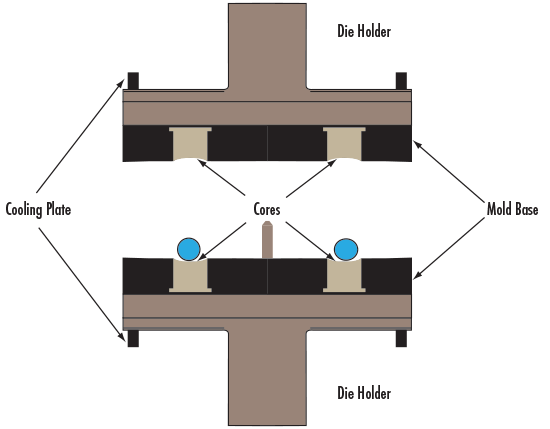
Abbildung 4: Präzisionspresse für Glasasphären
Präzisionspolitur
Standardmäßig werden Asphären durch Schleifen und Polieren hergestellt. Neue technische Fortschritte erlauben dabei eine bisher nicht erreichbare Genauigkeit. Vor allem passt die computergesteuerte Präzisionspolitur (Abb.5) automatisch die Werkzeugverweilzeiten so an, dass die Punkte stärker poliert werden, bei denen dies erforderlich ist. Wenn eine hochwertigere Politur benötigt wird, wird zur Bearbeitung der Oberfläche das magnetorheologische Polieren (MRF) verwendet (siehe Abbildung 6). Das MRF-Verfahren erlaubt ein hochpräzises Polieren in kürzerer Zeit als die Standardpolierverfahren, weil sich sowohl der Ort des Materialabtrags genau bestimmen lässt, als auch der Materialabtrag selbst schnell erfolgt. Zum Pressen von Asphären werden sehr teure Formen benötigt, wohingegen die Politur Standardwerkzeuge verwendet, so dass dieses Verfahren vor allem für die Prototypenfertigung und Kleinserien verwendet wird.
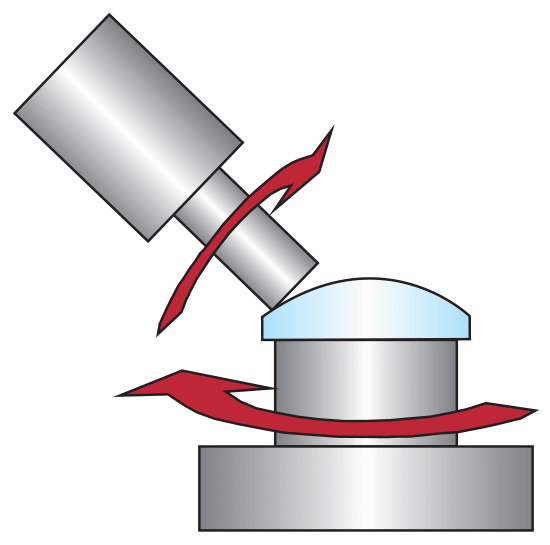
Abbildung 5: Computergesteuertes Polieren
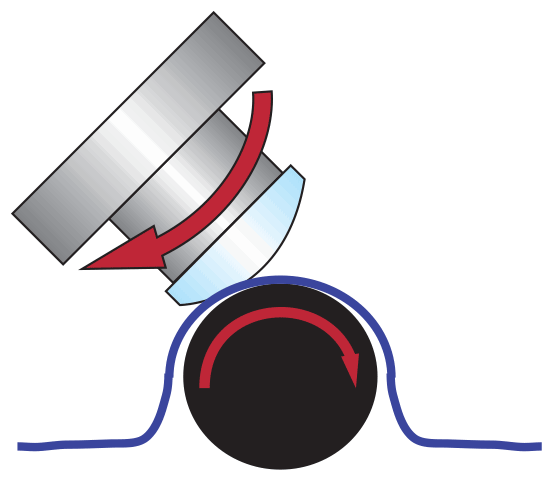
Abbildung 6: Magnetorheologisches Polieren (MRF)
Pressen von Hybrid-Asphären
Beim Pressen von Hybrid-Asphären wird zunächst eine normale sphärische Fläche, beispielsweise ein Achromat, verwendet, der dann in einer asphärischen Form in eine dünne Lage Photopolymer gepresst wird, um letztendlich eine asphärische Fläche zu erhalten. Bei diesem Verfahren werden diamantgeschliffene Asphärenformen und eine Optik aus Glas verwendet. Dabei spielt es keine Rolle, welche Art von Linse oder Doublett verwendet wird. Eine Photopolymer wird in die asphärische Form eingespritzt, darauf wird dann die Glaslinse gepresst. Die beiden Flächen werden zusammengedrückt und im UV-Licht bei Raumtemperatur ausgehärtet. Ein Beispiel aus dem EO-Sortiment ist der asphärischer Achromat, der die optischen Eigenschaften seiner Bestandteile vereint: Korrektur der chromatischen und sphärischen Aberration. Abbildung 7 zeigt eine Übersicht für die Fertigung einer Hybridlinse. Gepresste Hybridasphären eignen sich für Präzisionsanwendungen in großen Serien, bei denen die Stückzahl die Kosten für die Anfertigung des Werkzeugs rechtfertigt.

Abbildung 7: Pressen von Hybridasphären
Pressen von Kunststoffasphären
Als Ergänzung zu den oben erwähnten Fertigungsverfahren für Glas gibt es ein spezifisches Verfahren für Kunststoffe. Beim Pressen von Kunststoffasphären wird geschmolzener Kunststoff in eine asphärische Form eingespritzt. Da Kunststoff nicht thermisch stabil und nicht so druckbeständig wie Glas ist, muss er speziell behandelt werden, um eine vergleichbare Asphäre zu produzieren. Kunststoff hat dessen ungeachtet Vorteile aufgrund des geringen Gewichts, der einfachen Herstellung und kann mit Fassung produziert werden, so dass eine einteilige Komponente entsteht. Die Auswahl der Kunststoffe mit optischer Qualität ist begrenzt, die Vorteile bei Kosten und Gewicht veranlassen die Konstrukteure jedoch mitunter, Kunststoffasphären zu verwenden.
Vorteile der verschiedene Arten von Asphären
Da nicht bei allen Anwendungen die gleichen Linsen verwendet werden, spielt die Auswahl der richtigen Asphäre eine wichtige Rolle. Die Hauptfaktoren bei der Auswahl sind Stückzahlen und Kosten. Sobald diese beiden Parameter feststehen, können Sie die richtige Asphäre einfach auswählen.
Standardasphären sind sofort ab Lager bzw. mit kurzen Lieferzeiten für jede denkbare Anwendung lieferbar, sie sind jedoch nur in bestimmten Größen und mit bestimmten Brennweiten und Beschichtungsoptionen erhältlich. Wenn die Standardprodukte nicht ausreichen, ist die kundenspezifische Fertigung von Asphären als Prototyp, für die Vorproduktion oder die Serienfertigung möglich.
| Typ | Vorteil |
|---|---|
| Blankgepresste Asphären | Ideal für eine Produktion mit großen Stückzahlen, weil viele Linsen schnell produziert werden können und die Wartungskosten für das Werkzeug niedrig sind. |
| Polierte Asphären | Ideal für Prototypen und Kleinserien aufgrund der kurzen Lieferzeit und der geringen Werkzeugkosten. |
| Hybrid-Asphären | Aufgrund der Korrektur sowohl der sphärischen als auch der chromatischen Aberration ideal für Multispektralanwendungen. |
| Kunststoffasphären | Ideal für die Massenproduktion, da sie eine leichte, kostengünstige Alternative zu Glasasphären sind. |
Fertigungsmöglichkeiten kundenspezifischer Asphären
| Kommerziell | Präzise | Hochpräzise | |
|---|---|---|---|
| Durchmesserbereich | 10 – 150 mm | 10 – 150 mm | 10 – 150 mm |
| Toleranz Durchmesser | +0/-0,100 mm | +0/-0,025 | +0/-0,010 |
| Asphärischer Formfehler (P-V) | 3 μm | 1 μm | <0,06 μm* |
| Scheitelradius (asphärisch) | ±0,5% | ±0,1% | ±0,05% |
| Sag | 25 mm max | 25 mm max | 25 mm max |
| Typischer Steigungsfehler (Slope-Error) | 1 μm pro 1 mm window | 0,35 μm pro 1 mm window | 0,15 μm pro 1 mm window |
| Zentrierung (Strahlablenkung) | 3 arcmin | 1 arcmin | 0,5 arcmin |
| Toleranz Mittendicke | ±0,100 mm | ±0,050 mm | ±0,010 mm |
| Oberflächenqualität (Scratch Dig) | 80–50 | 40–20 | 10–5 |
| Messtechnik asphärische Oberflächen | Profilometrie (2D) | Profilometrie (2D & 3D) | Interferometrie |
* 1/10th wave at 632,8 nm, limited by design and/or metrology
Auswahlhilfe für Asphären
| Auswahlhilfe für Asphären | |
| Präzise geschliffene Asphären | |
|
Unsere präzise geschliffenen Asphären sind ideal für die anspruchsvollsten Anwendungen. Sie bieten hohe numerische Aperturen und eine beugungsbegrenzte Abbildung.
|
|
| Präzise gepresste Asphären | |
 Die präzise gepressten Asphären sind ideal für Anwendungen bei denen große Stückzahlen benötigt werden, z.B. Laserdiodenkollimation, Barcodescannen und optische Datenspeicherung.
|
|
| Farbkorrigierte Asphären | |
|
Wir bieten eine einzigartige Produktserie an, die sowohl eine Korrektur der sphärischen als auch der chromatischen Aberration bietet. Diese Serie ist ideal für Anwendungen bei denen eine nahezu beugungsbegrenzte Fokussierung über einen großen Wellenlängenbereich benötigt wird.
|
|
| Asphären für den IR Bereich | |
|
Von kleinen gepressten Asphären bis zu Asphären aus Germanium und Zinkselenid bieten wir Lösungen für das gesamte Infrarotspektrum.
|
























































weitere regionale Telefonnummern
ANGEBOTSTOOL
Geben Sie zum Starten die Produktnummer ein.
Copyright 2023 | Edmund Optics, Ltd Unit 1, Opus Avenue, Nether Poppleton, York, YO26 6BL, UK
Die Edmund Optics GmbH Deutschland fungiert als Handelsvermittler für die Edmund Optics Ltd. in Großbritannien.
Vertragspartner ist die Edmund Optics Ltd. in Großbritannien.