Thermische Eigenschaften von optischen Substraten

Thermischer Ausdehnungskoeffizient

Für Anwendungen, die anfällig für Temperaturschwankungen sind, sollte ein athermisches optisches System entwickelt werden. Athermische optische Systeme sind unempfindlich gegenüber Temperaturänderungen der Umgebung und die dadurch entstehende Defokussierung des Systems. Die Entwicklung eines athermischen Systems, das vom thermischen Ausdehnungskoeffizienten (CTE, auch Wärmeausdehnungskoeffizient) und der Änderung des Brechungsindex mit der Temperatur $ \left( \tfrac{\text{d} n}{ \text{d} T} \right) $ des Materials abhängt, ist besonders im IR-Bereich von hoher Bedeutung. 

Der thermische Ausdehnungskoeffizient ist ein allgemeiner Begriff für eines von drei Maßen für die Veränderung der Größe, der Fläche oder des Volumens eines Materials aufgrund einer Temperaturänderung. Lieferanten von optischem Glas und Optikdesigner geben jedoch nur den linearen Wärmeausdehnungskoeffizienten oder den Koeffizienten der linearen Wärmeausdehnung (CLTE, wie er in der Polymerindustrie abgekürzt wird) an, der wie folgt definiert ist:

$ \small{\alpha_{L}} $ ist der lineare CTE, $ \small{L} $ ist die Länge in einer Dimension, $ \small{T} $ ist die Temperatur und $ \tfrac{\text{d} L}{\text{d} T} $ ist der Kehrwert des Temperaturgradienten in Bezug auf die Dimension $ \small{L} $. 

 $ \small{\alpha_{A}}$ ist der Flächen-CTE, $ \small{A} $ ist die Fläche in zwei Dimensionen und $ \tfrac{\text{d} A}{\text{d} T} $ ist der Kehrwert des Temperaturgradienten in Bezug auf die Fläche. 

 $ \small{\alpha_{V}}$ ist der Volumen-CTE, $ \small{V} $ ist das Volumen in drei Dimensionen und $ \tfrac{\text{d} V}{\text{d} T} $ ist der Kehrwert des Temperaturgradienten in Bezug auf das Volumen. Für isotrope Werkstoffe, einschließlich der meisten Glas- und Metallwerkstoffe, ist die Beziehung zwischen den CTEs in Gleichung 4 dargestellt.

In der Praxis werden die Differentialterme für die Längen- und Temperaturänderung ($\small{\text{d}L}$ und $\small{\text{d}T}$, vor allem bei kleinen Temperaturänderungen) in der Regel gut angenähert durch die Differenzen ($\small{ \Delta L}$ und $\small{ \Delta T}$) in Gleichung 5.

(5)$$ \alpha_L \approx \frac{1}{L} \frac{\Delta L}{\Delta T} $$

Wird ein Objekt erwärmt, wird es aufgrund der höheren kinetischen Energie der Moleküle, aus denen das Objekt besteht, in der Regel größer. Es gibt jedoch einige wenige Ausnahmen, bei denen die Beziehung zwischen Temperatur und Länge umgekehrt ist, z. B. bei Wasser. Der lineare thermische Ausdehnungskoeffizient von Wasser wird unter 3,983°C negativ, sodass sich Wasser ausdehnt, wenn die Temperatur unter 3,983°C sinkt.

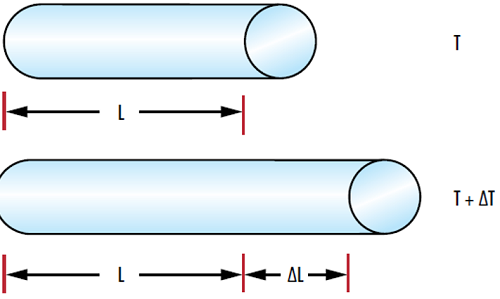
Abbildung 1: Temperaturänderungen $ \left( \small{ \Delta T \small} \right) $ führen zu einer Änderung der Länge eines Materials $ \left( \small{ \Delta L} \right) $, die vom thermischen Ausdehnungskoeffizienten des Materials abhängt.

Der lineare CTE wird in Einheiten von $ \tfrac{1}{ ˚ \text{C}}$ oder $ \tfrac{1}{ \text{K}}$ angegeben. Bei der Auswahl einer Optik für Ihre Anwendung muss der thermische Ausdehnungskoeffizient berücksichtigt werden, weil Größenänderungen der Optik die Ausrichtung und Spannung der Komponenten beeinflussen können. In Umgebungen, in denen Temperaturschwankungen auftreten, muss darauf geachtet werden, dass sich die Optik bei Erwärmung nicht ausdehnt. Eine Optik mit einem Durchmesser von 25 mm bei Raumtemperatur kann bei 300°C einen Durchmesser von 25,1 mm aufweisen, sodass die Halterung beschädigt oder Licht in eine unerwünschte Richtung abgelenkt und so die Punktstabilität oder Laserausrichtung beeinflusst werden kann. Aus diesem Grund ist im Allgemeinen ein kleiner thermischer Ausdehnungskoeffizient wünschenswert.

Temperaturkoeffizient des Brechungsindex

Der Temperaturkoeffizient des Brechungsindex $ \left( \tfrac{\text{d} n}{\text{d} T} \right) $ ist ein Maß für die Änderung des Brechungsindex in Abhängigkeit von der Temperatur. Der $ \tfrac{\text{d} n}{\text{d}T} $-Wert der meisten IR-Materialien ist Größenordnungen höher als der von Gläsern im sichtbaren Spektrum, sodass es zu großen Änderungen des Brechungsindex kommt. Ob der Brechungsindex von Gläsern mit steigender Temperatur zu- oder abnimmt, hängt vom jeweiligen Material ab, aber die meisten Gläser haben bei höheren Temperaturen einen höheren Brechungsindex.¹ Beim Design von athermischen Objektiven werden Gläser mit positivem und negativem Temperaturkoeffizienten kombiniert, um die Brechungsindexänderung des jeweils anderen Materials auszugleichen.

Die vollständige Gleichung für $ \tfrac{\text{d} n}{\text{d}T} $ eines Materials ist gegeben durch:

Dabei gilt:

$ \small{ T_0 }$ ist die Referenztemperatur (20℃)

$\small{T } $ ist die Temperatur in ℃

$\small{\Delta T}$ ist die Temperaturdifferenz $ \left( \small{T} - \small{T_0} \right)$

$\small{\lambda}$ ist die Wellenlänge des Lichts im Vakuum

$ \small{D_0, D_1, D_2, E_0, E_1,} $ und $ \small{\lambda} _{\small{\text{TK}}} $ sind alle empirisch ermittelten Materialkonstanten

$ \tfrac{\text{d} n}{\text{d} T} $ ist für reflektierende Optiken, abgesehen von geringfügigen Schwankungen der (qualitativen) Leistung aufgrund von Änderungen des Brechungsindex der Beschichtung, ohne Belang. $ \tfrac{\text{d} n}{\text{d} T} $ ist jedoch eine wichtige Kenngröße für transmittierende Optiken, da damit die Stabilität der Optiken bei Temperaturschwankungen bestimmt werden kann. Bei Laserstrahlen mit hoher Leistung, die auf eine Optik treffen, gibt es immer eine gewisse Absorption, sodass die Temperatur zunimmt. $ \tfrac{\text{d} n}{\text{d} T} $ bestimmt dann die Auswirkung auf die (qualitative) Leistung (Abbildung 2).

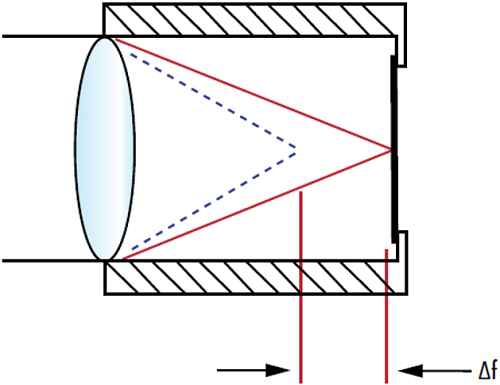
Abbildung 2: Die Änderung des Brechungsindex einer optischen Komponente abhängig von der Temperatur $ \left(  \tfrac{\text{d} n}{\text{d} T} \right) $ kann zu einer Verschiebung der Brennweite einer Linse $ \left( \Delta f \right) $ führen, sodass sich die Position des Fokuspunkts ändert.

Wärmeleitfähigkeit

Die Wärmeleitfähigkeit $ \left( \small{k} \right) $ eines Materials ist ein Maß für die Fähigkeit des Materials, Wärme abzuleiten (Abbildung 3). Sie wird üblicherweise in $ \tfrac{\text{W}}{ \left( \text{m} \, \cdot \, \text{K} \right)} $ oder $ \tfrac{\text{Btu}}{\left( \text{hr} \, \cdot \, \text{ft} \, \cdot \, \text{˚F} \right)} $ gemessen und wird verwendet, um den Wärmestrom zu definieren:

$ \small{Q} $ steht für die in der Zeit $ \small{t} $ übertragene Wärmemenge, die Einheiten von $ \tfrac{Q}{t} $ sind $ \tfrac{\text{J}}{\text{s}} $ oder $ \small{\text{W}} $. $ \small{A} $ ist die Querschnittsfläche des Substrats, $ \small{\Delta T} $ ist der Temperaturunterschied zwischen einer Seite des Materials und der anderen und $ \small{d} $ ist die Dicke des Materials.

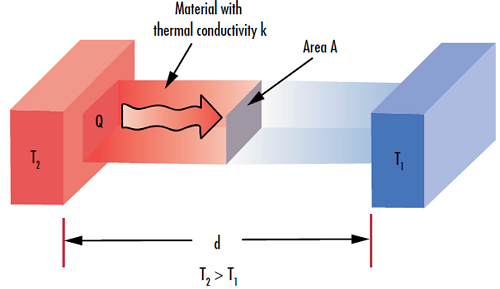
Abbildung 3: Die Wärmeleitfähigkeit eines Materials $ \left( \small{k} \right) $ definiert seine Fähigkeit Wärme $ \left( \small{Q} \right) $ durch eine bestimmte Dicke $ \left( \small{d} \right) $ zu übertragen.

Materialien wie Metalle mit einer hohen Wärmeleitfähigkeit können Wärme viel schneller ableiten als Materialien mit einer geringen Wärmeleitfähigkeit wie Gläser oder Kunststoffe. Da ein Haupteffekt der Übertragung von Laserstrahlung durch eine Optik die Umwandlung der Strahlungsenergie in Wärmeenergie ist, muss in Laseroptikanwendungen die Wärmeleitfähigkeit eines Materials bekannt sein, um die Energiebilanz im Umfeld der Optik bewerten zu können. Materialien, die bestimmte Wellenlängen nicht reflektieren oder durchlassen, z. B. Farbgläser und absorbierende Filter, absorbieren mehr Licht und erwärmen sich schneller. Bei einer Wärmeakkumulation in der Optik treten in kurzer Zeit Schäden auf, insbesondere wenn ein effektives Kühlsystem fehlt. Doch selbst mit einem effektiven Kühlsystem können nicht homogene optische Komponenten, deren Wärmeleitfähigkeit uneinheitlich ist, durch heiße Stellen im Material beschädigt werden. Ähnlich wie der Temperaturkoeffizient des Brechungsindex muss auch die Wärmeleitfähigkeit bei der Entwicklung von Hochleistungslasersystemen bekannt sein, um die zu erwartenden Auswirkungen auf die optische Leistung zu verstehen.

Literatur

1. “TIE-19: Temperature Coefficient of the Refractive Index.” Schott, Juli 2016.