Grundlagen der passiven Athermalisierung

Thermischer Defokus | Achromatische & athermische Duplet-Gleichungen | Grafische Methode zur Auswahl von achromthermen Glas- und Gehäusematerialien

Für Anwendungen, die zu Temperaturschwankungen neigen, ist es wichtig, ein athermisches optisches System zu entwickeln: ein optisches System, das unempfindlich gegen die thermische Veränderung der Umgebung und die daraus resultierende Defokussierung des Systems ist. Die Entwicklung eines athermischen Systems, das vom thermischen Ausdehnungskoeffizienten des Materials und der Änderung des Brechungsindex mit der Temperatur $ \left( \tfrac{\text{d}n}{\text{d}T} \right) $ abhängt, ist besonders im IR-Bereich von hoher Bedeutung. Der $ \tfrac{\text{d}n}{\text{d}T}$-Wert der meisten IR-Materialien ist Größenordnungen höher als der von Gläsern im sichtbaren Spektrum, sodass es zu großen Änderungen des Brechungsindex kommt. Darüber hinaus ist auch das Gehäusematerial empfindlich gegenüber thermischen Veränderungen und sollte bei der Erwägung eines athermischen Designs berücksichtigt werden.

Thermischer Defokus

Die Ausdehnung und das Zusammenziehen eines Materials aufgrund von Temperaturänderungen wird durch den Wärmeausdehnungskoeffizienten $ \small{\alpha} $ beschrieben, der die Einheit $ \small{10^{-6}} \tfrac{\text{m}}{\text{K}} $, $ \small{10^{-6}} \tfrac{\text{m}}{˚ \text{C}} $, $ \small{\tfrac{\text{ppm}}{\text{K}}} $, oder $ \small{\tfrac{\text{ppm}}{˚ \text{C}}} $. Die Längenänderung $ \small{ \left( L \right)} $ eines Materials aufgrund einer Temperaturänderung ist durch Gleichung 1 gegeben.

Thermische Defokussierung ist die Änderung der Fokusposition auf der Achse bei Temperaturänderungen aufgrund der Änderung des Brechungsindexes mit der Temperatur $ \left( \tfrac{\text{d}n}{\text{d}T} \right) $ und der Ausdehnung des Materials. Gleichung 2 beschreibt die Änderung der Brennweite einer Linse in Luft mit der Temperatur, wobei $ \small{\beta} $ der thermo-optische Koeffizient ist.

$ \small{\beta} $ kann mit Gleichung 3 ermittelt werden, wobei $ \small{\alpha_g} $ der thermischer Ausdehnungskoeffizient (CET) des Glases ist. Die Gleichung für $ \small{\beta} $ enthält üblicherweise einen Term für die Änderung des Brechungsindex der Luft mit der Temperatur, aber da dieser Term im Vergleich der Materialien $ \left( \tfrac{\text{d}n}{\text{d}T} \right) $ im IR klein ist, wurde er hier nicht berücksichtigt. Diese Näherung sollte im Sichtbaren nicht verwendet werden, da die Effekte der Luft einen größeren Einfluss auf den thermo-optischen Koeffizienten haben als im IR.

Für ein Objektiv, das in einem Gehäuse mit einem Wärmeausdehnungskoeffizienten $ \small{\alpha_h} $ montiert ist, ist die Änderung der Fokusposition eine Kombination aus der Änderung der Brennweite des Objektivs und der Änderung der Bildebenenposition aufgrund der Gehäuseausdehnung, wie in Gleichung 4 und Abbildung 1 dargestellt. Wenn die Änderung der Gehäuselänge gleich der Fokusänderung der Optiken ist, dann ist die Defokussierung gleich Null und das System wird als athermisch betrachtet.

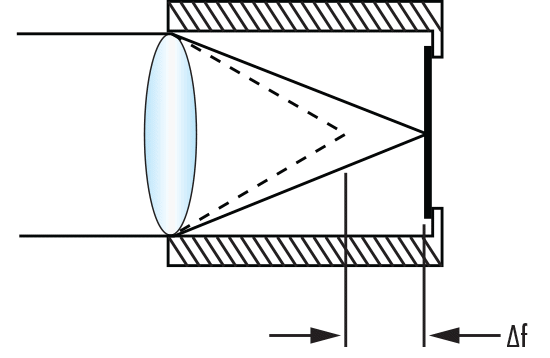
Defokussierung eines Objektivs in einem Metallgehäuse bei einer Temperaturänderung

Abbildung 1: Defokussierung $ \small{ \left( \Delta f \right)} $ eines Objektivs in einem Metallgehäuse bei einer Temperaturänderung $ \small{ \left( \Delta T \right)} $

Achromatische und athermische Duplet-Gleichungen

Ein gebräuchliches optisches Element ist das achromatische Duplet, das ein positives und ein negatives Element aus unterschiedlichen Materialien mit gleichen und entgegengesetzten Mengen an chromatischer Aberration zur Farbkorrektur verwendet. Unter der Annahme, dass sich ein Element in Luft befindet, ist die $\small{\nu}$-Zahl (inverse Dispersion) für ein beliebiges Wellenband, das durch die längste, kürzeste und mittlere Wellenlänge definiert ist, durch Gleichung 5 gegeben. Wenn die Gleichungen 6 und 7 erfüllt sind, ist das Ergebnis ein achromatisches Duplet. Die optimale Lösung ist die, welche zwei Elemente mit der größten Differenz der $\small{\nu}$-Zahl hat: $ \small{ \Delta \nu } $.

Ein größeres $ \small{ \Delta \nu } $ führt zu längeren Brennweiten (geringere Vergrößerung) und flacheren Radien (reduziert Abbildungsfehler und erhöht die optische Leistung). Mithilfe der Glaskarte ist die Auswahl eines Kron- und eines Flintglases, die einen großen Unterschied der $\small{\nu}$-Zahl aufweisen, sehr einfach. Analog können wir den Kehrwert des thermo-optischen Koeffizienten (Gleichung), üblicherweise die thermische $\small{\nu}$-Zahl genannt, in unseren achromatischen Gleichungen verwenden, um ein athermisches Duplet zu konstruieren (Gleichungen 8 und 9). Wenn wir ein Duplet entwickeln, bei dem die Gleichungen für das achromatische Duplet und das athermische Duplet alle erfüllt sind (Gleichungen 6-9), ist das Ergebnis ein achrothermisches System: ein System, das sowohl achromatisch als auch athermisch ist (Gleichung 10).

Durch Auftragen der thermischen $\small{\nu}$-Zahl $ \small{\left( \nu_T \right)} $ gegen die Farb-$\small{\nu}$-Zahl in einem Graph können wir visuell zwei Materialien identifizieren, die zur Entwicklung eines achrothermischen Systems verwendet werden können. Anhand der Gleichung für eine Gerade ($ \small{y = mx + b} $, wobei $ \small{m} $ die Steigung und $ \small{b} $ der y-Achsenabschnitt ist) sehen wir, dass, wenn wir den y-Achsenabschnitt gleich Null setzen und ein Material $ \left( \nu_1, \, \nu_{T1} \right) $ wählen, die Steigung $ \small{m} = \tfrac{\nu_{T1}}{\nu_1} $ ist. Aus der Duplet-Achrotherm-Gleichung wissen wir, dass die Steigung von zwei verschiedenen Materialien gleich sein sollte, um eine Farbkorrektur und Athermalisierung zu erreichen; jegliche zwei Materialien, die durch eine Linie verbunden werden können, die durch den Ursprung geht, liefern eine achrothermische Lösung. Wie in Abbildung 2 dargestellt, würden IG5 und AMTIR1 in Luft für das LWIR (8 - 12 μm) eine nahezu achrothermische Lösung darstellen. Bitte beachten Sie: Der Graph berücksichtigt nicht die Ausdehnung eines eventuellen mechanischen Gehäuses des Systems.

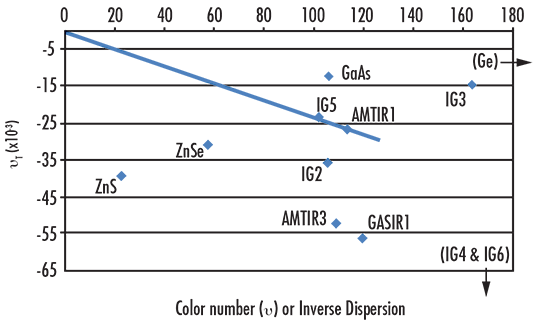
Beispielgraph mit ν<sub>T</sub> vs. ν für das LWIR

Abbildung 2: Beispielgraph mit $ \small{\nu_T} $ vs. $ \small{\nu} $ für das LWIR (8 - 12 µm)

Grafische Methode zur Auswahl von achrothermen Glas- und Gehäusematerialien

Eine Alternative zum Auftragen der thermischen $\small{\nu}$-Zahl $\left( \small{\nu_T} \right) $ gegen die Farb-$\small{\nu}$-Zahl beinhaltet das Auftragen des thermo-optischen Koeffizienten $\left( \small{\beta} \right) $ gegen die inverse Farb-$\small{\nu}$-Zahl.¹ Diese Methode hilft nicht nur bei der Identifizierung zweier möglicher optischer Materialien, sondern auch bei der Ermittlung des thermischer Ausdehnungskoeffizienten (CET) des Gehäusematerials, das für eine gefasste achrothermische Lösung erforderlich ist. Wie in Abbildung 3 dargestellt, liefert der y-Achsenabschnitt das erforderliche Gehäusematerial über eine Linie, die durch zwei Materialien verläuft und die y-Achse kreuzt. Für den Fall, dass ein einzelner Gehäusewerkstoff mit dem erforderlichen CET nicht verfügbar ist, kann der erforderliche CET mit einem Bimetallgehäuse oder einer alternativen mechanischen Befestigungslösung erreicht werden.

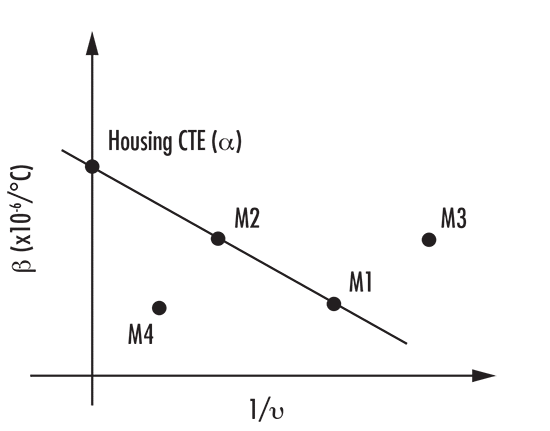
Athermische Glaskarte, bei der β gegen 1/ν aufgetragen ist

Abbildung 3: Athermische Glaskarte, bei der $ \small{\beta} $ gegen $ \tfrac{1}{\nu} $ aufgetragen ist

Es ist wichtig zu beachten, dass diese Methode immer noch davon ausgeht, dass das $ \tfrac{\text{d}n}{\text{d}T} $ von Luft im Vergleich zu dem der optischen Materialien gering ist; während dies für Infrarotsysteme zutrifft, muss das $ \tfrac{\text{d}n}{\text{d}T} $ von Luft für Systeme, die im sichtbaren Spektrum arbeiten, berücksichtigt werden. Weitere Details zu diesen und anderen grafischen Methoden zur Athermalisierung finden Sie in den angegebenen Quellen.

(1)$$\Delta L = \alpha L \Delta T $$

(1)

$$\Delta L = \alpha L \Delta T $$

(2)$$\Delta f = \beta f \Delta T $$

(2)

$$\Delta f = \beta f \Delta T $$

(3)$$\beta_r = \alpha_g - \frac{1 }{n -1} \frac{\text{d} n}{\text{d} T} $$

(3)

$$\beta_r = \alpha_g - \frac{1 }{n -1} \frac{\text{d} n}{\text{d} T} $$

(4)$$ \Delta f = f \left( \beta _{\text{Lens}} - \alpha_h \right) \Delta T $$

(4)

$$ \Delta f = f \left( \beta _{\text{Lens}} - \alpha_h \right) \Delta T $$

(5)$$ \nu = \frac{n_{\text{Mid}} -1 }{n_{\text{Short}} - n_{\text{Long}} } $$

(5)

$$ \nu = \frac{n_{\text{Mid}} -1 }{n_{\text{Short}} - n_{\text{Long}} } $$

(6)$$ \frac{\Phi_1}{\Phi}= \frac{\nu _1}{\nu_1 - \nu_2} $$

(6)

$$ \frac{\Phi_1}{\Phi}= \frac{\nu _1}{\nu_1 - \nu_2} $$

(7)$$ \frac{\Phi_2}{\Phi}= \frac{\nu _{2}}{\nu_{1} - \nu_{2}} $$

(7)

$$ \frac{\Phi_2}{\Phi}= \frac{\nu _{2}}{\nu_{1} - \nu_{2}} $$

(8)$$ \frac{\Phi_1}{\Phi}= \frac{\nu _{T1}}{\nu_{T1} - \nu_{T2}} $$

(8)

$$ \frac{\Phi_1}{\Phi}= \frac{\nu _{T1}}{\nu_{T1} - \nu_{T2}} $$

(9)$$ \frac{\Phi_2}{\Phi}= \frac{\nu _{T2}}{\nu_{T1} - \nu_{T2}} $$

(9)

$$ \frac{\Phi_2}{\Phi}= \frac{\nu _{T2}}{\nu_{T1} - \nu_{T2}} $$

(10)$$ \frac{\nu_1}{\nu_{T1}} = \frac{\nu_2}{\nu_{T2}} $$

(10)

(10)$$ \frac{\nu_1}{\nu_{T1}} = \frac{\nu_2}{\nu_{T2}} $$

Note: For these equations, the power of the elements in the system is at the center of the waveband being used and the index used is at the reference wavelength.

Referenzen

Katie Schwertz, Dan Dillon und Scott Sparrold. "Graphically Selecting Optical Components and Housing Material for Color Correction and Passive Athermalization." SPIE Proceedings Vol. 8486: Current Developments in Lens Design and Optical Engineering XIII, 11. Oktober 2012.
Katie Schwertz, Adam Bublitz und Scott Sparrold. "Advantages of Using Engineered Chalcogenide Glass for Color Corrected, Passively Athermalized LWIR Imaging Systems." SPIE Proceedings Vol. 8353: Infrared Technology and Applications XXXVIII, 31. Mai 2012.

Bibliographie

¹ Tamagawa, Yasuhisa, Satoshi Wakabayashi, Toru Tajime und Tsutomu Hashimoto. "Multilens System Design with an Athermal Chart." Applied Optics 34, Nr. 33 (1. Dezember 1994): 8009-013.

War dieser Inhalt nützlich für Sie?

Vielen Dank für die Bewertung dieses Textes!