Dispersion bei Ultrakurzpulslasern

Während die Auswirkung der Dispersion bei vielen Lasersystemen kaum eine Rolle spielt, ist die Dispersion in Ultrakurzpulslaseranwendungen äußerst problematisch. Ultrakurzpulslaser zeichnen sich durch kurze Pulsdauern in der Größenordnung von Picosekunden, Femtosekunden oder Attosekunden aus. Gemäß der heisenbergschen Unschärferelation weisen transformationsbegrenzte ultrakurze Pulse, die die untere Grenze ihrer Pulsdauer erreichen, eine große Wellenlängenbandbreite auf (Abbildung 1). Da diese Pulse mit großer Bandbreite über optische Medien übertragen werden, wird die Pulsdauer durch die chromatische Dispersion verlängert, was in Ultrakurzpulsanwendungen nachteilig ist.

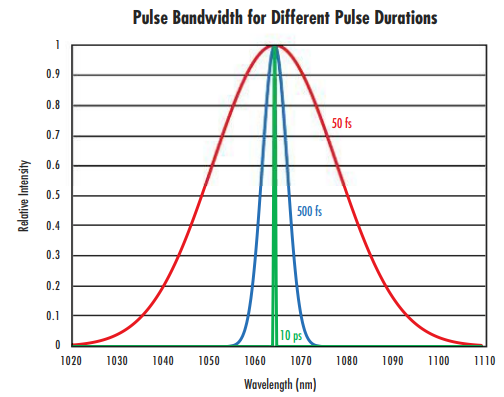
Abbildung 1: Mit abnehmender Pulsdauer von Ultrakurzpulslasern nimmt die Wellenlängenbandbreite zu.

Übersicht über chromatische Dispersion

Die Übertragung eines Laserpulses durch ein optisches Medium wird durch die Gruppengeschwindigkeit $ \small{v_g}$ beschrieben, d. h. die Abweichung der Phasengeschwindigkeit von Licht in einem Medium relativ zur Wellenzahl $ \small{k}$ des Mediums:

(1)$$ v_g = \left( \frac{\partial k}{\partial \omega} \right)^{-1} = c \left[ \frac{\partial}{\partial \omega} \left( \omega n \! \left( \omega \right) \right) \right] ^{-1} = \frac{c}{n \! \left( \omega \right) + \omega \frac{\partial n}{\partial \omega}} = \frac{c}{n_g \! \left( \omega \right)} $$

Dabei ist $ \small{\omega}$ die Kreisfrequenz des Lichts, $ \small{c} $ ist die Lichtgeschwindigkeit im Vakuum und $ \small{n} $ ist der Brechungsindex des Mediums. Die Wellenzahl $ \small{k}$ ist $ \tfrac{2 \pi}{\lambda}$ und wird bisweilen auch als Raumfrequenz der Welle bezeichnet. Der Unterschied zwischen Phasengeschwindigkeit und Gruppengeschwindigkeit ist in Abbildung 2 dargestellt.

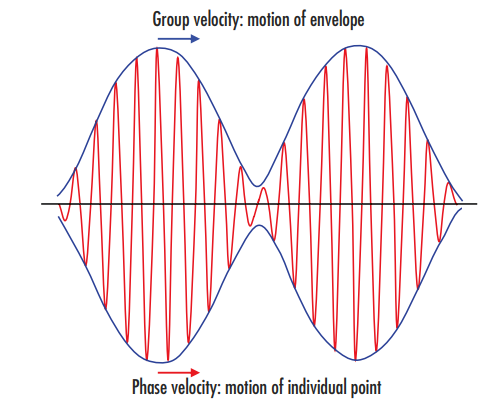
Abbildung 2: Die Gruppengeschwindigkeit definiert die Bewegung der Einhüllenden oder des Wellenzugs (blau hervorgehoben), während die Phasengeschwindigkeit die höherfrequente Bewegung der einzelnen Punkte der Welle selbst definiert (rot hervorgehoben).

Wenn Licht mehrerer Wellenlängen ein Material durchläuft, sind die längeren Wellenlängen (niedrige Frequenzen) geringfügig schneller als kürzere Wellenlängen, da die Gruppengeschwindigkeit von der Frequenz (oder Wellenlänge) abhängt.¹ Dies bewirkt eine spektrale Phasenabweichung der Wellenfront durch die spektrale Dispersion des Materials (genauso wie Licht, das ein Prisma durchläuft, in seine Farbbestandteile zerlegt wird). Während die Gruppengeschwindigkeit als erste Ableitung der Phasengeschwindigkeit in Bezug auf die Frequenz definiert ist, entspricht die Gruppengeschwindigkeitsdispersion der Ableitung der inversen Gruppengeschwindigkeit nach der Frequenz:

(2)$$ \text{GVD} = \frac{\partial}{\partial \omega} \left( \frac{1}{v_g} \right) = \frac{\partial}{\partial \omega} \left( \frac{\partial k}{ \partial \omega} \right) = \frac{\partial ^2 k}{\partial \omega ^2} $$

Die inverse Gruppengeschwindigkeit wird Dispersion erster Ordnung genannt, die Gruppengeschwindigkeitsdispersion Dispersion zweiter Ordnung. Genauso wie die Gruppengeschwindigkeit insofern der spektralen Dispersion ähnelt, als beide der ersten Ableitung des Brechungsindex nach der Wellenlänge oder Frequenz entsprechen, ähnelt die Gruppengeschwindigkeitsdispersion der partiellen Dispersion, da beide zweite Ableitungen in Bezug auf die Wellenlänge oder Frequenz sind. Die Verringerung der Gruppengeschwindigkeitsdispersion in einem optischen Design weist Ähnlichkeit mit der Optimierung der chromatischen Leistung auf. Der einzige Unterschied besteht darin, dass die Gruppengeschwindigkeit sowie die Gruppengeschwindigkeitsdispersion und nicht die zugehörige Abbe-Zahl sowie die partielle Dispersion das Designziel sind.

Die Gruppengeschwindigkeitsdispersion ist unabhängig von der Länge des jeweiligen optischen Mediums. Die Gruppenverzögerungsdispersion, das Produkt der Gruppengeschwindigkeitsdispersion mit der Länge, berücksichtigt die Länge des Mediums.

(3)$$ \text{GDD} = \text{GVD} \times \text{Length} $$

Die Gruppengeschwindigkeitsdispersion hängt wesentlich von der Wellenlänge ab und wird normalerweise in $ \tfrac{\text{fs}^2}{\text{mm}} $ Einheiten angegeben. Die Gruppengeschwindigkeitsdispersion von Quarzglas beträgt beispielsweise $ \small{+} 57 \tfrac{\text{fs}^2}{\text{mm}} $ bei 589,3 nm und $ \small{−} 26 \tfrac{\text{fs}^2}{\text{mm}} $ bei 1500 nm. Zwischen diesen Wellenlängen (bei ungefähr 1,3 μm) gibt es eine dispersionsfreie Wellenlänge, bei der die Gruppengeschwindigkeitsdispersion null ist. Abbildung 3 veranschaulicht die signifikante Änderung der Gruppengeschwindigkeitsdispersion von Quarzglas abhängig von der Wellenlänge. Bei der Glasfaserkommunikation wird die Gruppengeschwindigkeitsdispersion in der Regel als Ableitung in Bezug auf die Wellenlänge anstatt der Frequenz definiert und normalerweise in $ \tfrac{\text{ps}}{\text{nm km}} $ angegeben.

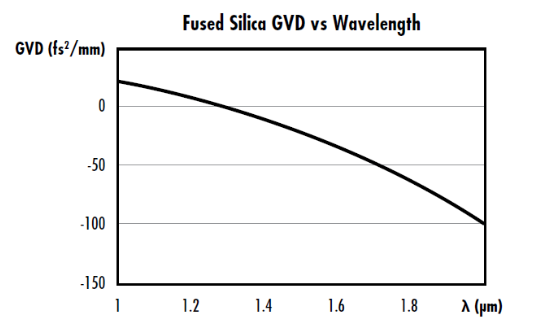
Abbildung 3: Gruppengeschwindigkeitsdispersion über der Wellenlänge für Quarzglas mit einer dispersionsfreien Wellenlänge von ca. 1,3 μm.

Ultrakurzpulslaser

Ultrakurzpulslaser sind aufgrund ihrer kurzen Pulsdauer und hohen Spitzenleistung hervorragend für eine Vielzahl von Anwendungen geeignet, z. B. biomedizinische Präzisionsanwendungen, Materialbearbeitung, Mikrobearbeitung, nichtlineare Mikroskopie und Bildverarbeitung sowie Kommunikation. Ultrakurzpulslaser ermöglichen bessere Abmessungstoleranzen bei der Materialbearbeitung und Mikrobearbeitung, sodass übliche Nachbearbeitungsschritte entfallen und Beschädigungen der Umgebung minimiert werden.² Genauso verringern Ultrakurzpulslaser das Risiko von inneren Verletzungen bei der Laserchirurgie und anderen medizinischen Anwendungen, sodass die Notwendigkeit von Anästhetika und Sterilisierung geringer wird.³ Die Pulse von Ultrakurzpulslasern werden erzeugt, wenn Lichtwellen mit einer großen Anzahl von Moden oder ganzzahligen Vielfachen der halben Lichtwellenlänge durch gleichphasige Überlagerung kohärent emittiert werden (Abbildung 4). Dies wird auch als Modenkopplung bezeichnet.

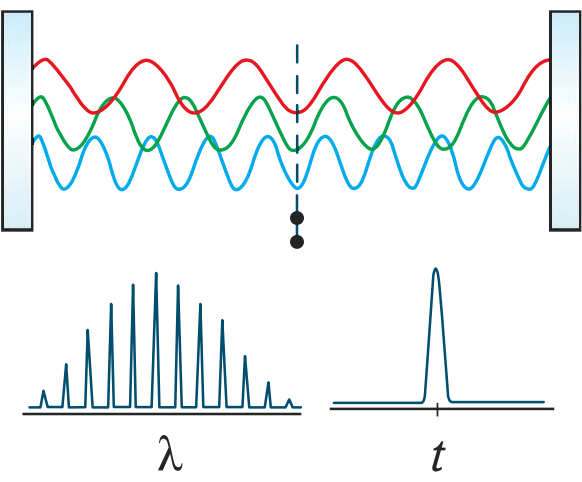
Abbildung 4: Durch Interferenz von kohärenten Wellen mit vielen Moden bei Modenkopplung entstehen Pulse mit einer ultrakurzen zeitlichen Breite, aber einer großen Wellenlängenbandbreite.

Die Abhängigkeit der Gruppengeschwindigkeitsdispersion von der Wellenlänge wirkt sich wegen ihrer großen Bandbreite erheblich auf ultrakurze Pulse aus, sodass die Pulsdauer von ultrakurzen Pulsen bei der Übertragung durch ein optisches System stark verbreitert wird (Abbildung 5). Das Ausmaß der Pulsverbreiterung von der Dauer des einfallenden Pulses $ \small{\tau_{\tiny{\text{In}}}} $ zur Pulsdauer am Ausgang $ \small{\tau_{\tiny{\text{Out}}}} $ hängt von der Gruppenverzögerungsdispersion ab (Abbildung 6):

(4)$$ \tau_{\tiny{\text{Out}}}= \tau_{\tiny{\text{In}}} \sqrt{1 + \left( \frac{4 \ln{\left( 2 \times \text{GDD} \right)} }{\tau_{\tiny{\text{In}}} ^2} \right)^2} $$

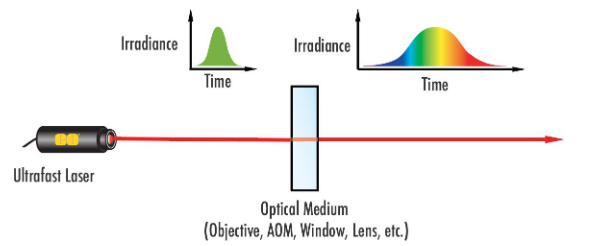
Abbildung 5: Die Dispersion bewirkt eine Verbreiterung von ultrakurzen Laserpulsen. AOM steht für „akustooptischer Modulator“. Dabei handelt es sich um eine Komponente, die Lasern die Aussendung eines gepulsten Strahls ermöglicht.

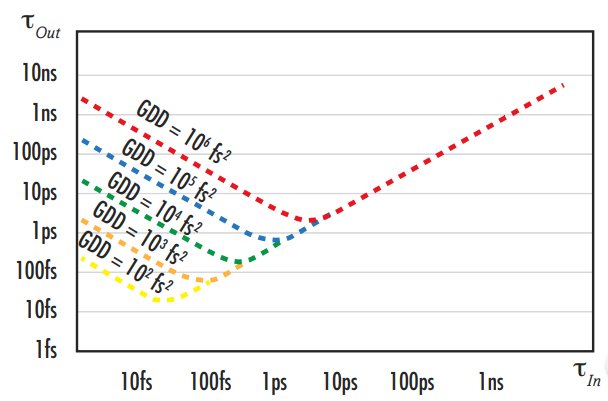
Abbildung 6: Veranschaulichung der zeitlichen Verbreiterung oder Vergrößerung der Pulsdauer eines ultrakurzen Femtosekundenpulses nach der Übertragung durch verschiedene optische Medien.

Die meisten optischen Medien weisen eine positive Dispersion auf. Die Phasengeschwindigkeit von langen Wellenlängen, die durch diese Medien übertragen werden, ist daher größer als die von kürzeren Wellenlängen, sodass die Pulsdauer größer wird (Abbildung 5). Dies wird als positiver Chirp bezeichnet. Ultrakurzpulslaser werden aufgrund ihrer großen Bandbreite durch Dispersion wesentlich stärker beeinflusst als andere Lasertypen.

Als Verfahren für die Messung der Gruppenverzögerung und der Gruppengeschwindigkeitsdispersion von optischen Ultrakurzpulsoptiken wird meistens die Weißlichtinterferometrie verwendet. Weitere Informationen finden Sie in unserem Anwendungshinweis Messtechnik für Laseroptiken.

Neben der Pulsverbreiterung kann die chromatische Dispersion auch dazu führen, dass die Brechungswinkel von optischen Oberflächen frequenzabhängig werden, sodass es zu einer winkelabhängigen Dispersion und frequenzabhängigen Weglängen kommt. Informationen zu Dispersionskompensationsverfahren zur Verbesserung der qualitativen Leistung von Ultrakurzpulslasersystemen finden Sie in unserem Anwendungshinweis Highly-Dispersive Mirrors application note.

Referenzen:

1. Ghatak, Ajoy, and K. Thyagarajan. “Optical Waveguides and Fibers.” University of Connecticut, 2000.
2. Mielke, Michael. “Ultrafast Lasers: Ultrashort Pulse Lasers Bring Cost-Efficient Precision to Micromanufacturing.” Laser Focus World, 8 Apr. 2015.
3. “The Benefits of Femtosecond Lasers and Why We Use Them.” Spindel Eye Associates, 16 May 2017, www.spindeleye.com/blog/2017/05/the-benefits-of-femtosecond-lasers-and-why-we-use-them/.

Vorheriger Abschnitt Nächster Abschnitt