Vergleich optischer Aberrationen

Aberrationen erkennen | Beispiele für Aberrationen

Optische Aberrationen (Abbildungsfehler) sind Abweichungen von einem perfekten mathematischen Modell. Wichtig ist hier der Hinweis, dass sie nicht durch physikalische, optische oder mechanische Mängel verursacht werden. Vielmehr können Aberrationen aufgrund der Wellennatur des Lichts durch die Form der Linse selbst oder die Anordnung der optischen Elemente innerhalb eines Systems hervorgerufen werden. Optische Systeme werden in der Regel unter Verwendung von Prinzipien der paraxialen Optik oder Optik erster Ordnung entworfen, um die Bildgröße und -position zu berechnen. Die paraxiale Optik berücksichtigt keine Aberrationen; sie behandelt das Licht als Strahl und lässt daher die Wellenphänomene, die Aberrationen verursachen, außer Acht. Eine Einführung in optische Aberrationen finden Sie unter Chromatic and Monochromatic Optical Aberrations.

Nach der Definition der verschiedenen Gruppen und Arten chromatischer und monochromatischer optischer Aberrationen besteht der schwierige Teil darin, diese in einem System zu erkennen, entweder durch Computeranalyse oder durch Beobachtung in der realen Welt, und dann das System zu korrigieren, um die Aberrationen zu reduzieren. In der Regel geben Optikdesigner ein System zunächst in eine optische Systemdesignsoftware wie Zemax® oder Code V® ein, um die Abbildungsleistung und die Aberrationen des Systems zu prüfen. Dabei ist es wichtig zu beachten, dass nach der Herstellung eines optischen Bauteils die Aberrationen durch Beobachtung des System-Outputs erkannt werden können.

Optische Erkennung von Aberrationen

Die Bestimmung der in einem optischen System vorhandenen Aberrationen ist nicht immer einfach, selbst in der Phase der Computeranalyse, da in den meisten vorhandenen Systemen häufig zwei oder mehr Aberrationen vorhanden sind. Optikdesigner nutzen eine Vielzahl von Werkzeugen, um Abbildungsfehler zu erkennen und zu korrigieren, dazu zählen u.a. computergenerierte Punktdiagramme, Wellenfrontdiagramme und Queraberrationsdiagramme. Punktdiagramme veranschaulichen, wie ein einzelner Lichtpunkt erscheinen würde, nachdem er durch das System abgebildet wurde. Wellenfrontdiagramme sind Darstellungen der Wellenfront im Verhältnis zur abgeflachten Wellenfront, wobei eine perfekte Welle in x-Richtung flach wäre. Queraberrationsdiagramme sind Darstellungen von Punkten des Strahlenfächers im Verhältnis zu den Pupillenkoordinaten. Das folgende Menü zeigt repräsentative Wellenfront- und Queraberrationsdiagramme für tangentiale (vertikale, y-Richtung) und sagittale (horizontale, z-Richtung) Ebenen mit $ \small{H = 1} $ für jede der folgenden Aberrationen: Verkippung $ \left( \small{W_{111}} \right) $, Defokus $ \left( \small{W_{020}} \right) $, sphärische $ \left( \small{W_{040}} \right) $, Koma $ \left( \small{W_{131}} \right) $, Astigmatismus $ \left( \small{W_{222}} \right) $, Bildfeldwölbung $ \left( \small{W_{220}} \right) $, und Verzeichnung $ \left( \small{W_{311}} \right) $. Wählen Sie einfach die gewünschte Aberration aus, um die einzelnen Abbildungen zu sehen.

Name der Aberration (Wellenfrontkoeffizient):

Abbildung 1: Airy-Scheibchen-Muster

Das Erkennen von Fehlern, insbesondere in der Designphase, ist der erste Schritt zur Korrektur. Warum will ein Optikdesigner Aberrationen korrigieren? Sein Ziel ist die Entwicklung eines beugungsbegrenzten Systems, das die bestmögliche Abbildungsleistung bietet. Die Abbildungsfehler beugungsbegrenzter Systeme werden durch die Größe der Airy-Scheibchen-Punktgröße oder die Größe des Beugungsmusters, das durch eine kreisförmige Apertur hervorgerufen wird, begrenzt (Abbildung 1).

Zur Berechnung der Größe des Airy-Scheibchens $ \small{\left( d \right)} $ kann Gleichung 1 herangezogen werden, wobei $ \small{\lambda} $ die im System verwendete Wellenlänge und f/# die Blendenzahl des Systems ist.

(1)$$ d = 2,44 \cdot \lambda \cdot \left( f/ \# \right) $$

BEISPIELE FÜR OPTISCHE ABERRATION

Nachdem ein System entworfen und hergestellt wurde, können Aberrationen festgestelllt werden, indem eine Punktquelle, z. B. ein Laser, durch das System abgebildet wird, um zu sehen, wie der einzelne Punkt in der Bildebene erscheint. Es können mehrere Aberrationen auftreten, im Allgemeinen gilt jedoch, dass je ähnlicher das Bild einem Punkt ist, desto wenigter Aberrationen liegen vor. Dies gilt unabhängig von der Größe, da der Punkt vom System vergrößert werden könnte. Die folgenden sieben Beispiele veranschaulichen das Strahlenverhalten, wenn die entsprechende Aberration die einzige im System ist, Simulationen von Bildern mit Abbildungsfehler unter Verwendung gängiger Testbilder (Abbildungen 2 - 4) und mögliche Korrekturmaßnahmen zur Minimierung der Aberration.

Die Simulationen wurden mit Code V® erstellt und sind zur besseren Veranschaulichung der induzierten Aberration übertrieben dargestellt. Es sei darauf hingewiesen, dass nur die Aberrationen erster und dritter Ordnung diskutiert werden, da die Korrektur von Aberrationen höherer Ordnung für die geringfügige Verbesserung der Bildqualität sehr komplex wird.

Abbildung 2: Verzeichnungstestbild mit Punktgitter fester Frequenz

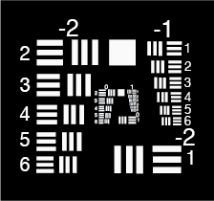
Abbildung 3: Negatives USAF 1951 Auflösungstestbild

Abbildung 4: Siemensstern

Verkippung – $\small{W_{111}}$
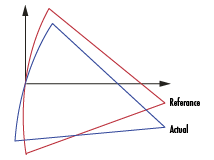Abbildung 5a: Darstellung der Verkippung	Abbildung 5b: Simulation der Verkippung
Charakterisierung Bild hat falsche Vergrößerung Verursacht durch die Verkippung der tatsächlichen Wellenfront gegenüber der Referenzwellenfront Erste Ordnung: $ \small{W_{111} = H \cdot \rho \cdot \cos{\left( \theta \right)}} $	Korrekturmaßnahmen Systemvergrößerung ändern

Defokussierung – $\small{W_{020}}$
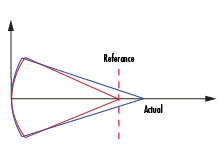Abbildung 6a: Darstellung der Defokussierungsaberration	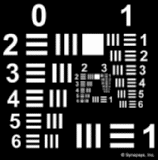Abbildung 6b: Simulation der Defokussierungsaberration
Charakterisierung Bild in falscher Bildebene Verursacht durch falsches Referenzbild Verwendung zur Korrektur anderer Aberrationen Erste Ordnung: $ \small{W_{020} = \rho ^2} $	Korrekturmaßnahmen System neu fokussieren, neues Referenzbild finden

Sphärisch – $\small{W_{040}}$
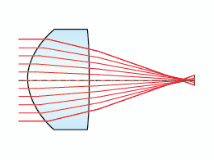Abbildung 7a: Darstellung der sphärischen Aberration	Abbildung 7b: Simulation der sphärischen Aberration
Charakterisierung Das Bild erscheint unscharf, Strahlen vom Rand werden an einem anderen Punkt fokussiert als Strahlen aus der Mitte Tritt bei allen sphärischen Optiken auf Aberration auf der Achse und außeraxiale Aberration Dritte Ordnung: $ \small{W_{040} = \rho ^4} $	Korrekturmaßnahmen Durch Defokussierung gegensteuern Asphärische Linsen verwenden Linsenaufteilung Formfaktor 1:PCX-Linse verwenden Hoher Index

Koma $\small{W_{131}}$
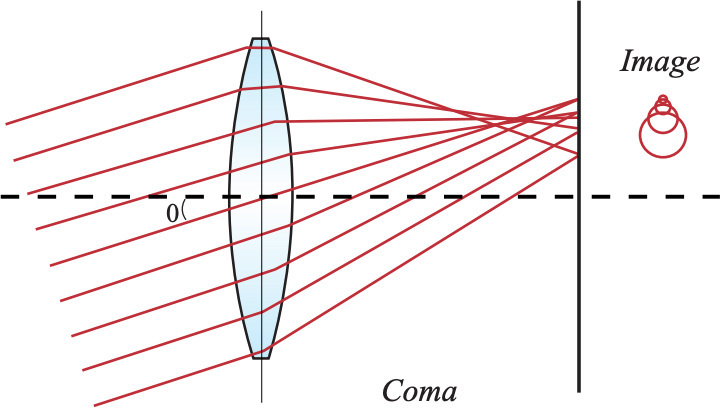Abbildung 8a: Darstellung der Koma-Aberration	Abbildung 8b: Simulation der Koma-Aberration
Charakterisierung Tritt auf, wenn sich die Vergrößerung in Abhängigkeit von der Position im Bild ändert Zwei Typen: Tangential (vertikal, Y-Richtung) und sagittal (horizontal, X-Richtung) Nur außeraxial Dritte Ordnung: $\small{W_{131} = H \cdot \rho ^3 \cdot \cos{\left( \theta \right)}} $	Korrekturmaßnahmen Verwendung einer Duplet-Linse mit Luftspalt mit Aperturblende in der Mitte

Astigmatismus – $\small{W_{222}}$
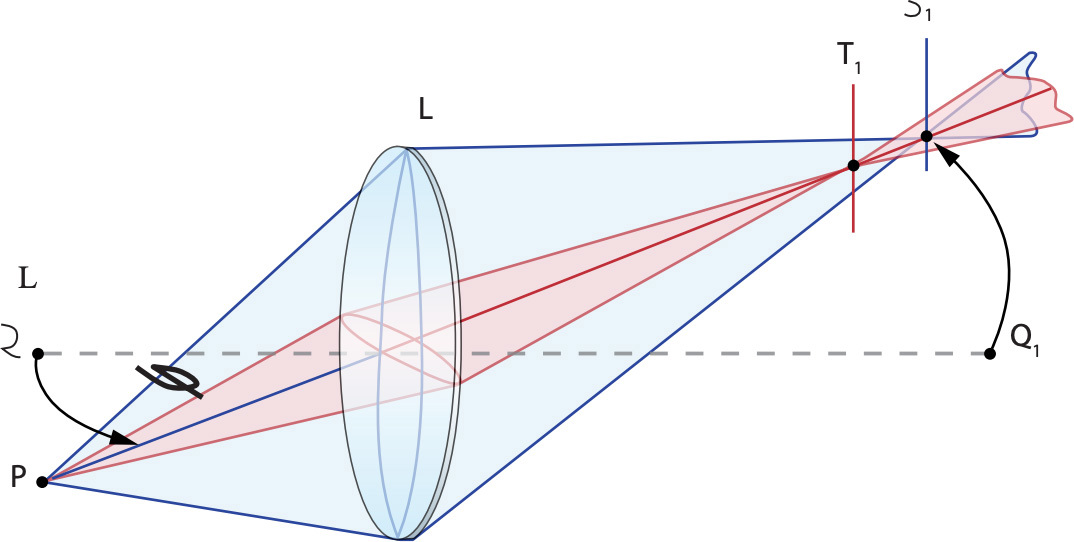Abbildung 9a: Darstellung der Astigmatismus-Aberration	Abbildung 9b: Simulation der Astigmatismus-Aberration
Charakterisierung Führt zu zwei Brennpunkten: Einer in horizontaler (sagittaler) und der andere in vertikaler (tangentialer) Richtung Die Austrittspupille erscheint außerhalb der Achse elliptisch, der Radius ist in einer Richtung kleiner Nur außeraxial Dritte Ordnung: $\small{W_{222} = H^2 \cdot \rho^2 \cos^2{\left( \theta \right)}}$	Korrekturmaßnahmen Durch Defokussierung gegensteuern Verwendung einer Duplet-Linse mit Luftspalt mit Aperturblende in der Mitte

Bildfeldwölbung – $\small{W_{220}}$
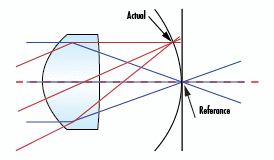Abbildung 10a: Darstellung der Bildfeldwölbungsaberration	Abbildung 10b: Simulation der Bildfeldwölbungsaberration
Charakterisierung Das Bild ist perfekt, aber nur auf der gewölbten Bildebene Verursacht durch die Abweichung vom Krümmungsradius der Optik Nur außeraxial Dritte Ordnung: $\small{W_{220} = H^2 \cdot \rho^2}$	Korrekturmaßnahmen Duplet-Linse mit Luftspalt verwenden

Verzeichnung $\small{W_{311}}$
Abbildung 11a: Darstellung der Verzeichnungsaberration	Abbildung 11b: Simulation der tonnenförmigen Verzeichnung Abbildung 11c: Simulation der kissenförmigen Verzeichnung
Charakterisierung Quadratischer Vergrößerungsfehler, Punkte auf dem Bild sind entweder zu nah oder zu weit vom Zentrum entfernt Positive Verzeichnung wird als tonnenförmige Verzeichnung, negative als kissenförmige Verzeichnung bezeichnet Nur außeraxial Dritte Ordnung: $ \small{W_{311} = H^3 \cdot \rho \cdot \cos{\left( \theta \right)}} $	Korrekturmaßnahmen Verringerung durch Platzierung der Aperturblende in der Mitte des Systems

Das Erkennen optischer Aberrationen ist sehr wichtig, um sie in einem optischen System zu korrigieren, denn das Ziel ist es, das System beugungsbegrenzt zu machen. Optische und bildgebende Systeme können mehrere Kombinationen von Aberrationen enthalten, die entweder als chromatisch oder monochromatisch eingestuft werden können. Die Korrektur von Abbildungsfehlern erfolgt am besten in der Designphase, wo Schritte wie das Verschieben der Aperturblende oder die Änderung des Typs der optischen Linse die Anzahl und Schwere (oder das Ausmaß) der Abbildungsfehler drastisch reduzieren können. Insgesamt bemühen sich Optikdesigner vor allem um die Verringerung der Aberrationen erster und dritter Ordnung, da die Verringerung der Aberrationen höherer Ordnung zu einer erheblichen Komplexität führt, die nur eine geringe Verbesserung der Bildqualität zur Folge hat.