Das Airy-Scheibchen und die Beugungsgrenze

Dies ist der Abschnitt 2.4 des Leitfadens zur Bildverarbeitung.

Vorheriger Abschnitt Nächster Abschnitt Blauer Pfeil nach rechts

Das Airy-Scheibchen

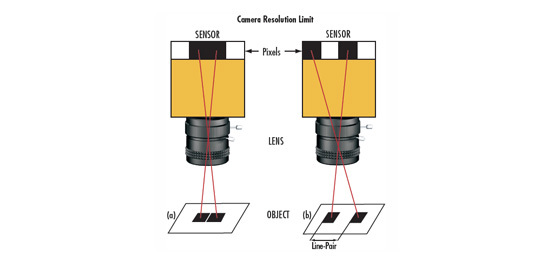
Wenn Licht durch eine beliebig große Blende fällt (jedes Objektiv hat eine endliche Blende), tritt Beugung auf. Das resultierende Beugungsmuster, ein heller Bereich in der Mitte umgeben von einer Reihe konzentrischer Ringe mit abnehmender Intensität, wird als Airy-Scheibchen bezeichnet (siehe Abbildung 1). Der Durchmesser dieses Musters hängt mit der Wellenlänge (λ) des verwendeten Lichts und der Größe der kreisförmigen Apertur zusammen und stellt den kleinste Punkt dar, auf den ein Lichtstrahl in diesem System fokussiert werden kann. Nahe beieinanderliegende Airy-Muster von verschiedenen Objektdetails beginnen sich zu überlappen (siehe Kontrast). Wenn die überlappenden Muster genug konstruktive Interferenz erzeugen, um den Kontrast zu verringern, können sie schließlich nicht mehr unterschieden werden. Abbildung 1 zeigt den Unterschied in der Punktgröße zwischen einem Objektiv, das auf f/2,8 eingestellt ist, und einem Objektiv, das auf f/8 eingestellt ist. Dieser Effekt wird mit zunehmender Verkleinerung der Pixel immer mehr zu einem Problem. Das Airy-Scheibchen $ \left( \varnothing_{\small{\text{Airy-Scheibchen}}} \right) $ oder die minimale Punktgröße kann mithilfe von Blendenzahl (f/#) und Wellenlänge (λ) abgeschätzt werden:

(1)$$ \varnothing _{\small{\text{Airy-Scheibchen}}} \approx 2,44 \times \lambda \times \left( \text{f} / \# \right) $$

(1)

$$ Ø_{\small{\text{Airy-Scheibchen}}} \approx 2,44 \times \lambda \times \left( \text{f} / \# \right) $$

Steigende Beugung bei einem geschlossenen Objektivs einer Blende

Abbildung 1: Die Beugung nimmt zu, wenn die Blende des Objektivs geschlossen wird (und die f/# zunimmt). Das obere Objektiv ist auf f/2,8 eingestellt, das untere Objektiv auf f/8.

Tabelle 1 zeigt den Airy-Scheibchendurchmesser für verschiedene Blendenzahlen bei Verwendung von grünem Licht (520 nm). Die kleinste erreichbare Punktgröße kann schnell die Größe von kleinen Pixeln überschreiten. Dies führt zu Schwierigkeiten und macht es manchmal unmöglich, das volle Auflösungsvermögen eines Sensors mit einem brauchbaren Kontrast zu erreichen. Des Weiteren sind hier keine Einschränkungen beim Linsendesign oder Fertigungsfehler bei der Herstellung der Linsenelemente oder der optischen Baugruppen berücksichtigt, die dazu führen können, dass der kleinste physikalisch mögliche Lichtfleck nicht erreicht werden kann und somit die Auflösungs- und Kontrastwerte verringert werden.

f/#	Airy-Scheibchendurchmesser [µm] bei einer Wellenlänge von 520 nm
2	2,54
2,8	3,55
4	5,08
5,6	7,11
8	10,15
11	13,96
16	20,30

Tabelle 1: Die minimale Punktgröße (oder das Airy-Scheibchen) nimmt mit der Blendenzahl zu und kann schnell die Pixelgröße übersteigen. Siehe Tabelle 1 im Abschnitt Auflösung für Beispiel zu Pixelgrößen.

Bitte beachten Sie: Dies sind theoretische Überlegungen, die als Grundlage für die Einschränkungsbetrachtung in einem optischen System dienen.

Die Beugungsgrenze

Jedes Objektiv hat eine obere Leistungsgrenze, die durch die Gesetze der Physik und das Airy-Scheibchen vorgegeben ist, die sogenannte Beugungsgrenze. Sie ist das theoretische maximale Auflösungsvermögen des Objektivs, angegeben in Linienpaaren pro Millimeter $ \left[ \small{\tfrac{\text{lp}}{\text{mm}}} \right] $. Ein perfektes Objektiv, das nicht durch sein Design eingeschränkt ist, wird trotzdem immer noch beugungsbegrenzt sein.

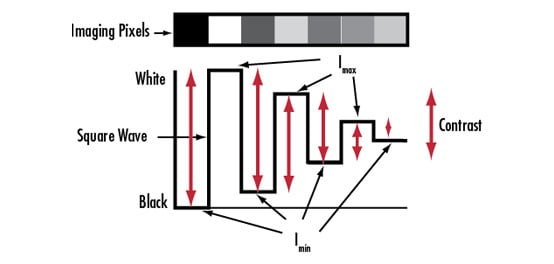
Die Beugungsgrenze ist der Punkt, an dem zwei Airy-Muster nicht mehr voneinander zu unterscheiden sind (Abbildung 2 im Abschnitt Kontrast). Die beugungsbegrenzte Auflösung, die oft als Grenzfrequenz eines Objektivs bezeichnet wird, wird mithilfe der Blendenzahl des Objektivs und der Wellenlänge des Lichts berechnet. Erfahren Sie mehr über die Blendenzahl (f/#) im Abschnitt Systemdurchsatz, Blende und numerische Apertur.

(2)$$ \xi_{\small{\text{Beugungsgrenze}}} = \frac{1}{\left( \text{f} / \# \right) \times \lambda} \times \left( \frac{1000 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} }{1\text{mm}} \right) $$

(2)

$$ \xi_{\small{\text{Beugungsgrenze}}} = \frac{1}{\left( \text{f} / \# \right) \times \lambda} \times \left( \frac{1000 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} }{1\text{mm}} \right) $$

Wenn die Beugungsgrenze erreicht ist, ist das Objektiv nicht mehr in der Lage höhere Frequenzen aufzulösen. Tabelle 2 zeigt die Beugungsgrenze für einen Kontrast von 0% bei den angegebenen Blendenzahlen. Tabelle 2 zeigt die Beugungsgrenze für einen Kontrast von 0% bei den angegebenen Blendenzahlen. Die Zahlen mögen auf den ersten Blick groß erscheinen, sind aber rein theoretischer Natur, sodass auch mehrere andere Faktoren berücksichtigt werden müssen. Wegen des inhärenten Hintergrundrauschens können bildgebende Sensoren keine Informationen bei oder nahe 0% Kontrast wiedergeben. Der Kontrast muss in der Regel 10% oder mehr betragen, um auf Standard-Bildsensoren erkannt zu werden. Um Probleme bei der Bildgebung zu vermeiden, wird sogar empfohlen, einen Kontrast von 20% oder höher bei der für die Anwendung wichtigen Auflösung anzustreben. Zusätzlich verringern Linsenaberrationen und Schwankungen in Verbindung mit Fertigungstoleranzen die Leistung.