Tiefenschärfe und Abbildungstiefe

Autoren: Gregory Hollows, Nicholas James

Dies ist der Abschnitt 3.4 des Leitfadens zur Bildverarbeitung.

Vorheriger AbschnittNächster Abschnitt

Aufgrund der Ähnlichkeiten der Bezeichnungen und Merkmale werden Tiefenschärfe und Abbildungstiefe häufig verwechselt. Hier eine kurze Definition: Die Tiefenschärfe bezieht sich auf die Bildqualität eines feststehenden Objektivs, wenn ein Objekt neu positioniert wird, während sich die Abbildungstiefe auf ein feststehendes Objekt und die Fähigkeit eines Sensors bezieht, den Fokus für verschiedene Sensorpositionen, einschließlich Neigung, beizubehalten.

Tiefenschärfe

Der Tiefenschärfebereich eines Objektivs ist seine Fähigkeit, ein gewünschtes Maß an Bildqualität (Ortsfrequenz bei einem bestimmten Kontrast) ohne Nachfokussierung beizubehalten, wenn die Objektposition nach vorne und hinten von der Ebene der besten Schärfe entfernt wird. Die Tiefenschärfe kann sich auch auf Objekte mit komplexer Geometrie oder unterschiedlichen Höhen beziehen. Wenn ein Objekt näher oder weiter als der eingestellte Fokusabstand eines Objektivs platziert wird, verschwimmt das Objekt und sowohl Auflösung als auch Kontrast nehmen ab. Die Angabe der Tiefenschärfe ist nur sinnvoll, wenn sie mit einer zugehörigen Auflösung und einem Kontrast verknüpft ist. Es können verschiedene Testbilder verwendet werden, um die Tiefenschärfe eines Bildgebungssystems direkt zu messen und zu vergleichen; einen Überblick über die Testbilder finden Sie unter Tests und Testbilder.

Auflösung und Tiefenschärfe

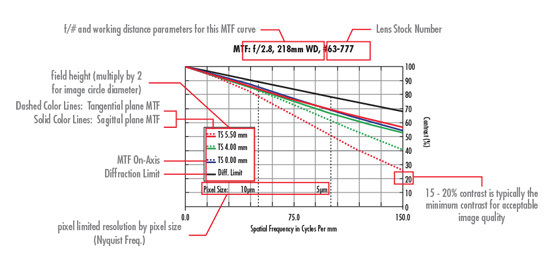
"Hat dieses Objektiv eine gute Tiefenschärfe?" Dies ist sehr schwer allgemein zu beantworten, ohne eine Objektdetailgröße oder Bildraumfrequenz anzugeben. Je kleiner das Detail, desto höher die benötigte Ortsfrequenz und desto kleiner die Tiefenschärfe, die das Objektiv erzeugen kann. Eine Tiefenschärfe-Kurve gibt an, welche Leistung ein Objektiv über eine vorgegebene Tiefe bei einer bestimmten Detailgröße zeigt (MTF-Kurven und Abbildungsleistung). Diese Diagramme berücksichtigen nicht nur die theoretischen Einschränkungen, die mit der Blendenzahl verbunden sind, sondern auch die Aberrationseffekte des Objektivdesigns.

In Abbildung 1 sind die Kontrastwerte (y-Achse) über einen Arbeitsabstandsbereich (x-Achse) bei einer festen Frequenz von 20$ \small{\tfrac{\text{lp}}{\text{mm}}} $ (Bilddetail) aufgetragen. Beachten Sie den Unterschied in der Tiefenschärfe zwischen Abbildung 1a bei Blende 2,8 und Abbildung 1b bei Blende 1,4. Beachten Sie weiterhin, dass aufgrund der Abnahme der Vergrößerung jenseits des besten Fokus mehr nutzbare Tiefenschärfe vorhanden ist als zwischen dem besten Fokus und dem Objektiv. Die Diagramme enthalten verschiedenfarbige Linien, die unterschiedliche Sensorpositionen kennzeichnen. Diese Arten von asymmetrischen Tiefenschärfe-Kurven sind typisch für Objektive mit fester Brennweite.

Abbildung 1: Tiefenschärfe-Kurven für ein Objektiv bei Blende 2,8 (a) und 4 (b).

Abbildung 2 zeigt das gleiche Objektiv wie Abbildung 1a, jedoch mit einem anderen Arbeitsabstand. Beachten Sie, dass sich bei längeren Arbeitsabständen die Tiefenschärfe vergrößert. Wenn das Objektiv auf unendlich weit entfernte Objekte fokussiert wird, tritt schließlich der hyperfokale Zustand ein. Bei dieser Entfernung erscheint alles gleich scharf.

Abbildung 2: Tiefenschärfe-Kurven für ein Objektiv mit Blende 2,8 bei 200 mm Arbeitsabstand (a) und 500 mm Arbeitsabstand (b). Hinweis: Bild (a) hat einen viel größeren Maßstab.

Auswirkung der Blende auf die Tiefenschärfe

Das Ändern des Blendenwerts eines Objektivs ändert die Tiefenschärfe, wie in Abbildung 3 dargestellt. In Abbildung 3 gibt es in jeder Zeichnung zwei Strahlenbündel. Das durch gestrichelte schwarze Linien dargestellte Bündel zeigt, wie gut das Objektiv fokussiert ist. Wenn sich ein Objekt von der besten Fokusposition entfernt (wo sich die gestrichelten Linien kreuzen), bewegen sich die Objektdetails in einen breiteren Bereich des Kegels. Je breiter die Ausdehnung des Kegels ist, desto mehr verschwimmt das Bild. Die Blendenzahl des Objektivs steuert, wie schnell sich der Kegel ausdehnt und wie viele Informationen oder Details in einer bestimmten Entfernung verschwimmen. Abbildung 3a zeigt ein Objektiv mit einer geringen Tiefenschärfe, während Abbildung 3b ein Objektiv mit großer Tiefenschärfe zeigt.

Abbildung 3: Geometrische Darstellung der Tiefenschärfe für Objektive mit hoher und niedriger Blendenzahl.

Der rote Kegel in Abbildung 3 ist eine Winkeldarstellung der Systemauflösung. Der Schnittpunkt der Linien des roten Kegels mit den gestrichelten schwarzen Linien definiert den Gesamtbereich der Tiefenschärfe. Je niedriger die Blendenzahl, desto schneller breiten sich die schwarzen Linien aus und desto geringer ist die Tiefenschärfe.

Bei kleineren Details (dargestellt durch einen kleineren roten Kegel), rücken die Kegelstrahlen in Abbildung 3a und 3b näher zusammen. Irgendwann führt dann eine zu starke Erhöhung der Blendenzahl dazu, dass kleinere Details aufgrund der Beugungsgrenze des Objektivs verschwimmen, da die Grenzauflösung des Objektivs umgekehrt proportional zur Blendenzahl ist. Dies bedeutet, dass eine Erhöhung der Blendenzahl zwar immer die Tiefenschärfe erhöht, aber die minimale auflösbare Detailgröße (selbst bei bester Fokussierung) abnimmt. Weitere Informationen über die Beugungsgrenze und ihre Beziehung zur Blendenzahl finden Sie unter Das Airy-Scheibchen und die Beugungsgrenze. Werden kurze Wellenlängen verwendet, kann die Auflösung teilweise wieder erhöht und erhalten werden. Erfahren Sie in MTF-Kurven und Abbildungsleistung mehr darüber, wie die Wellenlänge die Systemleistung beeinflussen kann. Beachten Sie, dass der Beugungseffekt in Abbildung 3 nicht zu sehen ist, aber hier als Hinweis erwähnt wird.

Wenn Objektive bei kurzen Arbeitsabständen fokussiert werden, führen die großen Kegelwinkel im Allgemeinen dazu, dass die Kegel sehr schnell auf beiden Seiten des besten Fokus divergieren, was zu einer begrenzten Tiefenschärfe führt. Bei Objekten in größerem Arbeitsabstand werden die Kegelwinkel flacher und die Tiefenschärfe wird größer.

Beispiel: Blendeneffekte auf Objektebene

Abbildung 4a zeigt das Strahlenbündel in der Mitte eines zu untersuchenden Objekts bei Blende 2,8 (a) und Blende 8 (b). Die vertikalen Linien stellen 2-mm-Schritte vom besten Fokus aus dar. Auf jeder vertikalen Linie stellt ein Quadrat die Detailgröße eines einzelnen Pixels dar. Abbildung 4a zeigt, dass mit zunehmender Breite des Strahlenbündels mehr Strahlen das Detail verfehlen. In Abbildung 4b dehnt sich das Bündel langsamer aus und die Strahlen treffen alle auf das Detail, das für jede dargestellte Tiefe größer als der Bündeldurchmesser ist.

Abbildung 4: Darstellung des Strahlenbündels in der Mitte eines zu untersuchenden Objekts bei Blende 2,8 (a) und Blende 8 (b).

Abbildung 5 zeigt das gleiche Konzept wie Abbildung 4, aber die Kegel stellen mehrere Punkte im Bildfeld dar. Jedes Detail und jede nachfolgende Lücke stellen ein Linienpaar dar. Die Überlappung in den Bündeln in Abbildung 5a zeigt, dass die Informationen schneller ineinander übergehen als in Abbildung 5b und wie zwei unterschiedliche Objektdetails aufgrund einer niedrigeren Blendenzahl miteinander verschwimmen können. In Abbildung 5b tritt dies aufgrund der höheren Blendenzahl des Objektivs nicht auf.

Abbildung 5: Eine Zeichnung der Strahlenbündel über einen Teil des mittleren Bildfelds bei Blende 2,8 (a) und Blende 8 (b).

Abbildungstiefe - für Fortgeschrittene

Die Abbildungstiefe ist das bildseitige Komplement der Tiefenschärfe und bezieht sich darauf, wie sich die Schärfe auf der Sensorseite des Objektivs ändert, wenn der Sensor bewegt wird, während das Objekt an der gleichen Position bleibt. Die Abbildungstiefe charakterisiert, wieviel Kippung und Neigung zwischen der Bildebene des Objektivs und der Sensorebene selbst toleriert wird. Mit abnehmender Blendenzahl nimmt auch die Abbildungstiefe ab, was den Einfluss der Neigung auf die Schärfe über den gesamten Sensor erhöht. Ohne eine aktive Ausrichtung wird es immer eine gewisse Abweichung in der Orthogonalität zwischen dem Sensor und dem verwendeten Objektiv geben; Abbildung 6 veranschaulicht dies. Es wird oft allgemein angenommen, dass Probleme mit der Abbildungstiefe nur bei großen Sensoren auftreten.

Tatsächlich ist das Problem jedoch unabhängig von der Sensorgröße. Wie die Herleitung in Gleichung 3 zeigt, ist die Abbildungstiefe, $\delta $, stark von der Anzahl der Pixel, $ p $, abhängig und hat wenig mit der Array- bzw. Pixelgröße, $ s $, zu tun. Mit zunehmender Pixelzahl der Sensoren tritt das Problem deutlicher auf. Besonders in vielen Zeilenkamera-Anwendungen wird aufgrund großer Arrays und niedriger Blendenzahlen die Notwendigkeit einer sorgfältigen Ausrichtung zwischen Objekt, Objektiv und Sensor deutlich.

Abbildung 6: Wie sich die Sensorneigung in Bezug auf die optische Achse auf die Abbildungstiefe auswirkt, auf Pixelebene (a) und auf Sensorebene (b).

Auswirkungen der Sensorneigung

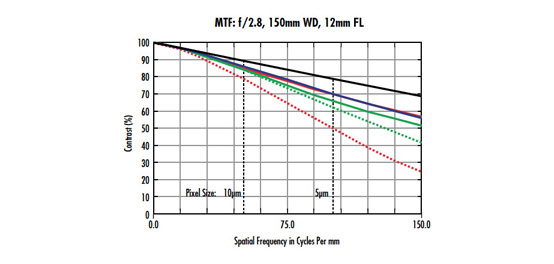
Abbildung 7 zeigt Graphen für ein Objektiv mit 35 mm Brennweite und Beleuchtung bei 470 nm. Bei Abbildung 7a beträgt die Blende 2,8 und bei Abbildung 7b 5,6. Beide Graphen zeigen Frequenzen bis 150$ \small{\tfrac{\text{lp}}{\text{mm}}} $—dies ist die Nyquistgrenze eines Sensors mit 3,45 µm großen Pixeln. Es ist leicht zu erkennen, dass die Abbildungsleistung in Abbildung 7a weitaus besser ist als die in Abbildung 7b. Die Verwendung des Objektivs bei Blende 2,8 bietet also die höchste Abbildungsqualität bei einer bestimmten Objektebene. Wie im vorherigen Abschnitt beschrieben, wirkt sich die Sensorneigung jedoch negativ auf die erzeugte Bildqualität aus. Je höher die Anzahl der Pixel, desto ausgeprägter ist der Effekt.

Abbildung 7: MTF-Kurven für ein Objektiv mit 35 mm Brennweite bei Blende 2,8 (a) und 5,6 (b). Beachten Sie, dass beide Objektive nahezu die Beugungsgrenze erreichen.

In Abbildung 8 wird die Abbildungstiefe für die beiden Fälle in Abbildung 7 analysiert. In beiden Fällen befindet sich die ganz rechte vertikale Linie im besten Fokus für das gesamte Bildfeld. Jede der schrägeren Linien links vom besten Fokus liegt 12,5 µm näher an der Rückseite des Objektivs. Diese Linien simulieren die Positionen der Pixel unter der Annahme einer Neigung/Kippung von 12,5 µm bzw. 25 µm von der Mitte zur Ecke des Sensors. Das blaue Strahlenbündel steht für die Bildmitte und die gelben und roten Strahlenbündel für die Ecken des Bildes. Die gelben und roten Bündel haben einen Abstand von einem Zeilenpaar auf dem Sensor unter der Annahme von 3,45 µm großen Pixeln. Beachten Sie in Abbildung 8a, dass es schon bei Blende 2,8 bei einer Verkippung um 12,5 µm ein Überlaufen zwischen den gelben und roten Strahlenbündeln gibt. Bei einer Verkippung von 25 µm deckt das rote Bündel nun zwei volle Pixel ab und auch etwa die Hälfte des gelben Bündels. Dies verursacht erhebliche Unschärfen. In Abbildung 8b bleiben bei Blende 5,6 die gelben und roten Strahlenbündel auch bei einer Verkippung von 25 µm innerhalb eines Pixels. Beachten Sie, dass sich die Position des blauen Pixels nicht ändert, da die Neigung/Kippung auf dieses Pixel zentriert ist.

Abbildung 8: Strahlenbündel des gleichen Objektivs mit 35 mm Brennweite bei Blende 2,8 (a) und Blende 5,6 (b) im Bildraum. Das blaue Strahlenbündel befindet sich in der Mitte des Bildes, das rote und das gelbe Strahlenbündel befinden sich in den Ecken des Bildes.

Abbildung 9 zeigt die Änderung der MTF-Kurven in den Bildecken für das 35-mm-Objektiv unter der Annahme einer Verkippung um 25 µm, wie in Abbildung 8 dargestellt. Abbildung 9a zeigt die neue Leistung des Objektivs bei Blende 2,8; beachten Sie die starke Abnahme der Abbildungsleistung verglichen mit Abbildung 7a. Abbildung 9b zeigt die Leistungsverschlechterung bei Blende 5,6, die im Vergleich zu Abbildung 9a gering ist. Der wichtigste Punkt aber ist, dass das Objektiv bei Blende 5,6 nun das Objektiv bei Blende 2,8 übertrifft. Der Nachteil des Objektiveinsatzes bei Blende 5,6 ist die dreimal geringere Lichtmenge im Vergleich zu Blende 2,8, was bei Hochgeschwindigkeitsanwendungen oder Zeilenscans problematisch sein kann. Noch ein letzter Punkt: Wird der Sensor um seine Mitte gekippt, kommt es sowohl am oberen als auch am unteren Rand des Sensors (und den entsprechenden Punkten im Bildfeld) zu einem Leistungsabfall, da sich die Strahlenbündel nach dem besten Fokus wieder ausdehnen. Es ist weiterhin wichtig zu wissen, dass keine zwei Kamera- und Objektivkombinationen identisch sind. Beim Aufbau mehrerer Systeme kann sich der Effekt in unterschiedlichem Ausmaß zeigen.

Abbildung 9: MTF-Kurven eines Objektivs mit 35 mm Brennweite bei Blende 2,8 (a) und Blende 5,6 (b) und mit 25 μm Versatz durch Bildebenenverkippung.

Um diese Probleme zu umgehen, müssen Kameras und Objektive mit engeren Toleranzen verwendet werden. Einige Objektive haben Mechanismen zur Kippsteuerung für Sensoren, um eine Sensorneigung zu verhindern. Beachten Sie, dass einige Zeilensensoren eine Senke haben können, d. h. sie sind nicht vollständig flach. Dies kann nicht durch die Kippsteuerung gemildert oder beseitigt werden.

Passende Produkte

Tiefenschärfetester DOF 5 - 15

Vorheriger AbschnittNächster Abschnitt

Weiterführende Informationen

 Anwendungshinweis

Tests und Testbilder

 Anwendungshinweis

MTF-Kurven und Abbildungsleistung

 Anwendungshinweis

Die Modulationstransferfunktion (MTF)