Objektivauswahl - erweiterte Informationen

Dies ist der Abschnitt 6.3 des Leitfadens zur Bildverarbeitung.

Im vorangegangenen Abschnitt über die Objektivauswahl wurde das Objektiv in erster Linie als letzte zu wählende Komponente des Bildverarbeitungssystems gesehen. In diesem Abschnitt wird die Auswahl von Objektiv und Kamera ganzheitlich betrachtet, indem beide gleichzeitig ausgewählt werden und geschaut wird, was für die jeweilige Anwendung wichtig ist. Wir betrachten ein Beispiel, bei dem ein 2D-Barcode aus einer Entfernung von 200 mm abgebildet werden muss (siehe Abbildung 1).

Abbildung 1: Bild des 2D-Barcodes, der aus einer Entfernung von 200 mm abgebildet werden muss.

Der erste Schritt bei der Auswahl eines Objektivs ist die genaue Betrachtung des zu untersuchenden Objekts. Was sind die wichtigsten Details? Wie groß sind diese Details? Wie viele Pixel brauche ich, um das zu beobachtende Detail so abzubilden, dass meine Bildverarbeitungssoftware richtig funktioniert?

Der beste Ansatzpunkt ist oft die Größe des Details und die Pixelabdeckung. Bei dem Barcode in Abbildung 1 ist dies recht einfach. Die Größe des wichtigsten Details beträgt 100 µm, wobei zwischen den einzelnen Details ein Leerraum von mindestens 100 µm liegt. In Frequenzen ausgedrückt ergeben sich somit 5$ \small{ \tfrac{\text{lp}}{\text{mm}}} $ (siehe Auflösung für eine genauere Erläuterung) im Objektraum. Diese Zahl ist das erste Puzzlestück bei der Bestimmung der erforderlichen Vergrößerung des Objektivs.

Als nächstes muss das gesamte Bildfeld (FOV) betrachtet werden. Nicht nur die Größe des Barcodes selbst, sondern auch ausreichend Platz für Positionsabweichungen innerhalb des FOV muss berücksichtigt werden. Die Größe des Barcodes ist 25 mm x 25 mm, bei einem FOV von 35 mm wäre sicherlich ausreichend Puffer vorhanden. In diesem speziellen Beispiel ist es wichtig, dass jedes Detail des Barcodes mindestens auf drei Pixeln abgebildet wird. Da die Größe der Details des Barcodes 100 µm beträgt, müssen also 33 µm der Objektebene auf ein Pixel projiziert werden.

An diesem Punkt können verschiedene Kameras näher betrachtet werden, um herauszufinden, ob dies möglich ist. Um die Kosten gering zu halten, kann es wichtig sein, mit einer möglichst kleinen Auflösung zu beginnen. Heutzutage bedeutet dies in der industriellen Bildverarbeitung oft eine Auflösung von 0,3 MP oder eine VGA-Auflösung (640x480). Das Seitenverhältnis der Sensoren beträgt 4:3. Das benötigte Bildfeld ist jedoch 1:1, was bedeutet, dass die kleinere Sensorseite (480 Pixel) dem 35-mm-Bildfeld entsprechen muss und die längere Sensorseite einen größeren Bereich als nötig abbildet und es wahrscheinlich ungenutzte Pixel geben wird.

Somit werden 480 Pixel auf eine Fläche von 35 mm verteilt, jedes Pixel entspricht also 110 µm im Objektraum. Die Kamera ist damit für diese Anwendung unzureichend und es wird eine etwa 3-fach bessere Auflösung benötigt. Wenn man die Rechnung noch einmal mit einem Sensor mit 1600x1200 Pixeln mit 4,5 µm Pixelgröße durchgeht, werden 29 µm auf jedes Pixel abgebildet, was ausreichend ist. Aber wie hängt das Ganze mit dem Bildraum und der Kamera mit Objektiv zusammen? An dieser Stelle muss das System mit der Vergrößerung verknüpft werden.

Da der verwendete Sensor Pixel mit einer Größe von 4,5 µm hat, sind die Sensorabmessungen 7,2 mm x 5,4 mm. Unter Verwendung der Gleichung 4 im Abschnitt Objektivauswahl - grundlegende Informationen ergibt sich eine erforderliche Vergrößerung von 0,15X. Anhand dieser Vergrößerung kann nun bestimmt werden, welches Objektiv benötigt wird und welche Auflösung das Bildgebungssystem erreichen muss, um den Barcode korrekt abzubilden. Da bereits ein Sensor ausgewählt wurde, kann nun Gleichung 3 aus Objektivauswahl - grundlegende Informationen verwendet werden, um die Brennweite des Objektivs zu bestimmen. Nach Gleichung 3 beträgt die erforderliche Brennweite 30 mm bei einem Arbeitsabstand von 200 mm. Die erforderliche Vergrößerung (0,15X) kann auch mit einem 25-mm-Objektiv aus 230 mm Entfernung erreicht werden und dies ist in diesem Fall eine passende Lösung. Nun ist ein vorläufiges Objektiv ausgewählt worden, aber erreicht es auch die erforderliche Auflösung?

Die erforderliche Auflösung im Objektraum beträgt 5$ \small{ \tfrac{\text{lp}}{\text{mm}}} $. Rechnet man dies in den Bildraum um, indem man durch den Vergrößerungsfaktor dividiert, sind 33$ \small{ \tfrac{\text{lp}}{\text{mm}}} $ erforderlich, um das Objekt richtig abzubilden. Diese Zahl muss mit zwei Zahlen abgeglichen werden: der Nyquistfrequenz des Sensors und der Modulationstransferfunktion (MTF) des verwendeten Objektivs. Weitere Informationen über die Nyquistfrequenz finden Sie im Abschnitt Auflösung. Gleichung 1 beschreibt die Nyquistfrequenz eines Sensors wie folgt:

(1)$$ \xi _{\small{\text{Nyquist}}} = \frac{1}{2 \times s} $$

(1)

$$ \xi _{\small{\text{Nyquist}}} = \frac{1}{2 \times s} $$

Dabei ist s die Pixelgröße. Unter Verwendung von Gleichung 1 hat ein Sensor mit 4,5 µm großen Pixeln eine Nyquistfrequenz von 111$ \small{ \tfrac{\text{lp}}{\text{mm}}} $. Da dies größer ist als die erforderlichen 33$ \small{ \tfrac{\text{lp}}{\text{mm}}} $, ist diese Kamera eine gute Wahl. Anfangs haben wir die Bedingung festgelegt, dass jeweils drei Pixel ein Detail abbilden müssen, und somit ist die Nyquistfrequenz des Sensors jetzt 3x höher als die erforderliche Frequenz. Diese Überlegungen wurden hier der Vollständigkeit halber erwähnt.

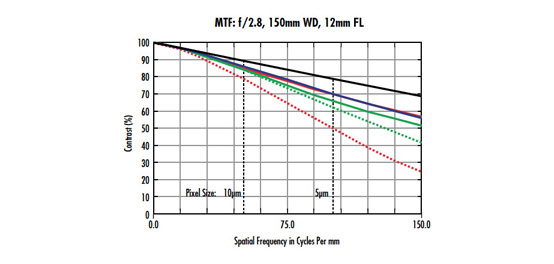
Die MTF-Kurve für ein 25-mm-Objektiv der C-Serie mit fester Brennweite bei einem Arbeitsabstand von 166 mm ist in Abbildung 2 dargestellt (weitere Informationen zum Lesen einer MTF-Kurve finden Sie unter Die Modulationstransferfunktion (MTF)). Ein Blick auf die Kurve zeigt, dass das 25-mm-Objektiv bei 33$ \small{ \tfrac{\text{lp}}{\text{mm}}} $ einen Kontrast von etwa 83% erreicht, was mehr als ausreichend ist, um eine gute Abbildung zu erzielen.

MTF-Kurve eines 25-mm-Objektivs der C-Serie mit fester Brennweite, das für dieses Beispiel eine mehr als ausreichende Auflösung erreicht.

Abbildung 2: MTF-Kurve eines 25-mm-Objektivs der C-Serie mit fester Brennweite, das für dieses Beispiel eine mehr als ausreichende Auflösung erreicht.

Als allgemeine Faustregel gilt, dass ein Objektiv einen Mindestkontrast von 20% haben muss, um ein Detail richtig aufzulösen. Somit besitzt das gewählte Objektiv mehr als genug Auflösung, um den Barcode ausreichend gut abzubilden.

Dies ist nur die Spitze des Eisbergs bei der Auswahl eines Objektivs für eine bestimmte Anwendung. Die MTF wird von mehreren Faktoren beeinflusst (ausführlich erklärt in MTF-Kurven und Abbildungsleistung) und die Verwendung ist nicht immer ganz einfach. Der folgende Abschnitt befasst sich nun eingehender mit dem Objektiv und mit der Frage, wie gut ein Objektiv zu einer Kamera passt.

Die sich ändernde Leistung eines Objektivs

Die Objektivhersteller sind in der Lage, maßgeschneiderte MTF-Kurven zu erstellen, die auf der Art der Verwendung des Objektivs basieren. Im obigen Barcode-Beispiel wurde die MTF des 25-mm-Objektivs herangezogen, um festzustellen, ob die Kontrastwiedergabe für den abgebildeten Barcode ausreichend ist. Wir werden dies nun anhand eines weiteren Beispiels mit demselben Objektiv vertiefen, um zu zeigen, dass die Dinge nicht immer so einfach sind, wie sie im ersten Moment erscheinen.

Abbildung 3 zeigt zwei verschiedene MTF-Kurven desselben 25-mm-Objektivs mit fester Brennweite bei gleichem Arbeitsabstand (Vergrößerung 0,76), aber unterschiedlichen Blendenzahlen und Wellenlängenbereichen. Die beiden Kurven unterscheiden sich deutlich voneinander. Die wichtigste Erkenntnis aus diesem Beispiel ist, dass die MTF-Kurven auf den technischen Datenblättern alleine nicht unbedingt ausreichen, um die Leistung eines Objektivs über seinen gesamten Einsatzbereich hinweg zu erklären.

Die MTF eines hochauflösenden 25-mm-Objektivs bei verschiedenen Einstellungen, was die Wichtigkeit eines Vergleichs der verschiedenen Objektivkurven unterstreicht.

Abbildung 3: Die MTF eines hochauflösenden 25-mm-Objektivs bei verschiedenen Einstellungen, was die Wichtigkeit eines Vergleichs der verschiedenen Objektivkurven unterstreicht.

Auf der Grundlage der MTF eines bestimmten Objektivs kann die minimale auflösbare Detailgröße im Objektraum bestimmt werden. MTF-Kurven sind jedoch immer für den Bildraum angegeben, was bedeutet, dass die Bildrauminformationen in Objektrauminformationen umgewandelt werden müssen. Glücklicherweise ist dies über eine einfache Skalierung mit der Vergrößerung möglich. Das folgende Beispiel veranschaulicht, wie diese Berechnungen durchgeführt werden können, wobei die Kurven in Abbildung 3 als Ausgangspunkt dienen. Wenn man ein Kontrastminimum von 20% annimmt, kann das Objektiv der ersten MTF-Kurve 250$ \small{ \tfrac{\text{lp}}{\text{mm}}} $ im Bildraum auflösen, nämlich die Frequenz auf der Kurve, die 20% Kontrast entspricht. Unter Verwendung von Gleichung 2 wird die Pixelgröße (oder in diesem Fall die Bildraumauflösung
$ \small{\xi _{\small{\text{Bildraum}}}} $ von einer Frequenz in eine Objektgröße umgewandelt) wie folgt berechnet:

(2)$$ \xi_{\small{\text{Bildraum}}} = 250 \tfrac{\text{lp}}{\text{mm}}= \frac{1000 \tfrac{\large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} }{\text{mm}} }{2 \times s} \therefore s = 2\large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} $$

(2)

$$ \xi_{\small{\text{Bildraum}}} = 250 \tfrac{\text{lp}}{\text{mm}}= \frac{1000 \tfrac{\large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} }{\text{mm}} }{2 \times s} \therefore s = 2 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} } $$

Die Skalierung mit der Vergrößerung (0,076X) ergibt:

(3)$$ \frac{2 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} }{0.076X} = 26 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} \text{ ist die minimale Detailgröße im Objektraum} $$

(3)

$$ \frac{2 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} }{0.076X} = 26 \large{\unicode[Cambria Math]{x03BC}} \normalsize{\text{m}} text{ ist die minimale Detailgröße im Objektraum} $$

Im Vergleich dazu kann das Objektiv mit der Kurve am unteren Rand des Graphs in Abbildung 3 nur ein Objekt mit einer Größe von 282 µm sicher abbilden (unter Verwendung der gleichen Berechnungen wie im obigen Beispiel). In diesem Beispiel wird davon ausgegangen, dass die genaue Kamera/der Sensor noch nicht ausgewählt wurde, sodass die Optik die begrenzende Komponente des Abbildungssystems ist. Hätte man sich vor dem Objektiv für einen Kamerasensor entschieden, müsste das Objektiv die Pixelgröße des verwendeten Sensors auflösen können.

Bei einer Kamera mit dem Sensor IMX250 von Sony mit 3,45 µm großen Pixeln kann unter Verwendung von Gleichung 2 eine Bildraumauflösung von 144,9$ \small{ \tfrac{\text{lp}}{\text{mm}}} $ ermittelt werden. Betrachtet man die MTF-Kurve, so erreicht das Objektiv bei dieser Frequenz einen Kontrast von über 40%, was für die meisten Anwendungen mehr als ausreichend ist. Wenn man jedoch die gleiche Berechnung wie in Gleichung 3 anwendet, um in den Objektraum zu skalieren, entsprechen 3,45 µm Pixel nur einem 45 µm großen Objekt, was bedeutet, dass der Sensor die begrenzende Komponente im System wäre, da das Objektiv eine Auflösung von 26 µm im Objektraum erreicht. All diese Überlegungen müssen bei der Bestimmung des richtigen Objektivs für eine bestimmte Anwendung angestellt werden, um die optimale Lösung für ein Bildverarbeitungsproblem zu finden.

Vorheriger Abschnitt Nächster Abschnitt

Weiterführende Informationen

Anwendungshinweis