Einfluss der Oberflächenebenheit von Laserspiegeln

Lasersysteme erfordern oft äußerst präzise optische Komponenten wie Spiegel und Linsen, deren Spezifikationen an die Grenzen der Fertigungsmöglichkeiten stoßen. Bei der Entwicklung eines optischen Systems, in dem ein Laser verwendet werden soll, sollte realistisch betrachtet werden, was im gewünschten Preisrahmen herstellbar ist. Wenn klar ist, welche Spezifikationen entscheidend und welche zwar gewünscht, aber unnötig sind, kann Zeit und Geld gespart werden. Je nach Anwendung können für ein Lasersystem kundenspezifische optische Komponenten erforderlich sein oder auch nicht. In diesem Text wird anhand einer Simulation erläutert, wie sich die Ebenheit einer Spiegeloberfläche auf die Größe des Fokuspunkts eines gaußschen Laserstrahls auswirkt, der sich durch ein simuliertes Lasermaterialbearbeitungssystem ausbreitet.

Der Text ist für jedes Lasersystem mit einem oder mehreren Laserspiegeln von Bedeutung. Um die Effizienz von Lasersystemen zu maximieren, werden Laserspiegel in der Regel mit ionenstrahlgesputterten (IBS) Beschichtungen oder aufgedampften Beschichtungen versehen. IBS-Beschichtungen sind beliebte Spiegelbeschichtungen, da sie eine extrem hohe spektrale Leistung aufweisen, was bedeutet, dass sie sehr hohe Reflexionsgrade erreichen können. Allerdings wird die Oberfläche, auf die sie aufgebracht werden, sehr stark beansprucht, was zu einer Verformung der Spiegeloberfläche führen kann, die nur durch eine ausgleichende Beschichtung auf der Rückseite der Optik oder einen langwierigen Kühlprozess verhindert werden kann. Aufgedampfte Beschichtungen hingegen üben nur eine geringe Belastung auf die Spiegeloberfläche aus, ihre spektrale Leistung ist jedoch geringer als die von IBS-Beschichtungen. In diesem Text werden die Auswirkungen von Beschichtungen zwar nicht direkt untersucht, aber die simulierten Spiegelkrümmungen entsprechen in etwa den Krümmungen, die beim Spiegel durch die symmetrischen Spannungen einer IBS-Beschichtung entstehen.

Optische Grenzwerte und Richtlinien

Krümmungsradius

Ebenheit und Krümmung der Oberfläche beziehen sich beide auf die Form der Spiegeloberfläche. Während die Ebenheit die Abweichung der Oberfläche von ihrer Nennform ist, wird die Krümmung als Kehrwert des Krümmungsradius definiert (Gleichung 1).

(1)$$ C = \frac{1}{R} $$

Da bei dieser Simulation der Krümmungsradius R benötigt wird, muss er aus mehreren anderen Abmessungen und Eigenschaften des Spiegels bestimmt werden. Zunächst wird davon ausgegangen, dass der Spiegel eine sphärische Krümmung aufweist, was bei Beschichtungen mit Spannung häufig der Fall ist, und dass die maximale Sag-Abweichung oder Pfeilhöhendifferenz genau gleich der Oberflächenebenheit SF ist (Gleichung 2).

(2)\begin{align} \text{Sag} & = \text{SF} \left[ \text{Wellen} \right] \\ & = \text{SF} \left[ \lambda \right] \end{align}

Wenn ein Strahl von einem einzigen Spiegel reflektiert wird, ist die Ebenheit der Oberfläche gleich dem reflektierten Wellenfrontfehler oder der Wellenfrontverzerrung. Sie wird in der Regel in Einheiten von Ringen oder Wellen angegeben und somit ergibt sich für die Oberflächenebenheit eines Spiegels ein positiver reeller Bruch oder ganzzahliges Vielfaches der Wellenlänge des verwendeten Lichts. Das Erweitern der Gleichung für die Sag-Abweichung erfordert eine genaue Beachtung der Semantik. Für Gleichung 3 wird der halbe Durchmesser der freien Apertur des Spiegels, ρ, benötigt.

(3)$$ R - \sqrt{R^2 - \rho^2} = \text{SF} $$

Für eine genaue Simulation in Zemax OpticStudio ist es wichtig zu beachten, dass es sich hier um die freie Apertur handelt, da es auch einen mechanischen halben Durchmesser gibt, der einfach die Hälfte des Optikdurchmessers ist und die freie Apertur nicht berücksichtigt. Über die Ebenheit der Oberfläche und den halben Durchmesser der freien Apertur kann der Krümmungsradius bestimmt werden (Gleichung 4).

(4)$$ R = \frac{1}{2} \left[ \text{SF} + \frac{\rho ^2}{\text{SF}} \right] $$

Da die Sag-Abweichung des Spiegels um viele Größenordnungen geringer ist als der Radius des Spiegels, ist der Beitrag des ersten Terms zum Krümmungsradius unbedeutend. Es ist daher sinnvoll, die parabolische Näherung zu verwenden, um Gleichung 4 in Gleichung 5 umzuwandeln und zu vereinfachen.

(5)$$ R \approx \frac{1}{2} \times \frac{\rho ^2}{\text{SF}} $$

Da sich die Krümmung umgekehrt proportional zum Krümmungsradius verhält, ist die Krümmung direkt proportional zur Ebenheit der Oberfläche. Dies ist ein wichtiger Punkt, da in unserem Beispiel die Spiegelkrümmung durch Änderung der Oberflächenebenheit verändert wird. Ein Spiegel mit einem Durchmesser von 25 mm hat einen mechanischen halben Durchmesser von 12,5 mm. Bei einer freien Apertur von 85% beträgt der halbe Durchmesser der freien Apertur des Spiegels (ρ) 10,625 mm. Bei einer Oberflächenebenheit von λ/10 und einer Wellenlänge von 1064 nm beträgt der Krümmungsradius etwa 5,3 × 105 mm und die Krümmung 1,9 × 10-6 mm-1.

Die Beugungsgrenze

Die Beugungsgrenze des fokussierten Punkts, die durch die Gleichung des Airy-Scheibchens beschrieben wird, kann verwendet werden, um die Untergrenze des Punktdurchmessers zu bestimmen. Sie wird als d bezeichnet und mithilfe der Wellenlänge des Lichts, λ, der Brennweite der Sammellinse, f, und der Größe oder dem Durchmesser des Strahls, D, ermittelt. Diese Untergrenze wird unter der Annahme bestimmt, dass die Sammellinse eine perfekte, paraxiale Linse ist, frei von jeglicher Aberration (Gleichung 6).

(6)$$ d \approx 2,44 \frac{f \, \lambda }{D} $$

Ein Laserstrahl mit 1064 nm und einem Durchmesser von 5 mm, der von einer paraxialen Linse mit einer Brennweite von 100 mm fokussiert wird, hat z. B. einen Durchmesser des Airy-Scheibchens von ca. 52 μm. Der Strahl kann nicht auf kleinere Punkte fokussiert werden, ohne dass eine Linse mit größerer Brechkraft verwendet wird. Da es keine perfekten, aberrationsfreien paraxialen Linsen gibt, wird der Lichtpunkt in der Realität höchstwahrscheinlich größer als der ermittelte Wert sein. Die Gleichung des Airy-Scheibchens liefert somit die untere Grenze, die sogenannte Beugungsgrenze, bis zu der ein Punkt theoretisch fokussiert werden kann.

Simulation mit Zemax OpticStudio & Ergebnisse

Die Simulation zur Prüfung der Auswirkungen der Spiegelkrümmung auf die Größe des fokussierten Strahls wurde in Zemax OpticStudio 18.9 erstellt. Das Modell verwendet einen Gaußstrahl mit einem Durchmesser von 2,5 mm und einer bestimmten Wellenlänge, der ein System aus sechs identischen Spiegeln (mit denselben Durchmessern und Oberflächenebenheiten) und drei Linsen von Edmund Optics durchläuft, wie in Abbildung 1 dargestellt.

Dieses simulierte Strahlaufweitungssystem besteht aus sechs identischen Spiegeln mit variabler Krümmung, PCV-Linse #48-049 und PCX-Linse #48-281 als 5X-Strahlaufweiter und PCX-Linse #37-817 als Kondensorlinse.

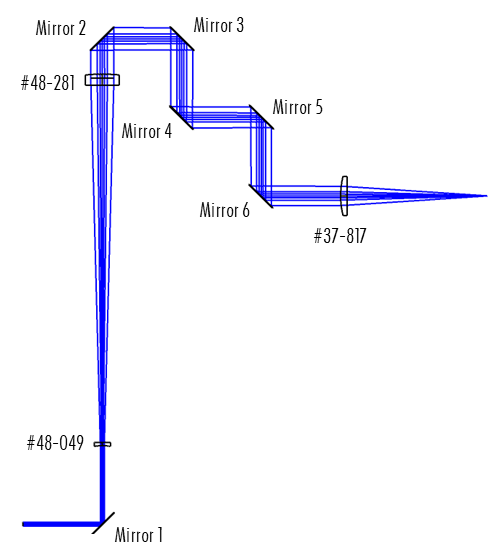
Abbildung 1: Dieses simulierte Strahlaufweitungssystem besteht aus sechs identischen Spiegeln mit variabler Krümmung, PCV-Linse #48-049 und PCX-Linse #48-281 als 5X-Strahlaufweiter und PCX-Linse #37-817 als Kondensorlinse.

Unter der Annahme, dass die freie Apertur einer Optik 85% ihres Durchmessers betragen sollte, haben die Spiegel in dieser Simulation einen mechanischen halben Durchmesser von 12,5 mm und einen halben Durchmesser der freien Apertur von 10,625 mm. Dieser Durchmesser wurde gewählt, um sicherzustellen, dass das Strahlenbündel auf jeden Fall innerhalb der freien Apertur der zweiten Linse im Strahlaufweiter liegt. In einer realen Anwendung würden viel größere Durchmesser für diese Strahlgröße gewählt werden, um das Abschneiden der Ränder des Gaußstrahls zu vermeiden. Der 5X-Strahlaufweiter besteht aus den Linsen #48-049 und #48-281 von Edmund Optics. Die Spiegel 2 bis 6 wurden in einem Abstand von 50 mm zueinander angebracht, um den optischen Pfad zu falten und so die Platzverhältnisse in einem echten Lasersystem zu simulieren. Der Abstand zwischen den beiden Linsen, die den Strahlaufweiter bilden, sowie der Abstand zwischen dem letzten Spiegel und der Kondensorlinse wurden optimiert, um den Strahl in der endgültigen Fokusebene zu fokussieren und die geometrischen Punktgrößen für den fokussierten Strahl bei unterschiedlichen Spiegelkrümmungen zu erhalten.

Um die Punktgröße bei unterschiedlichen Ebenheitswerten, aber gleicher Wellenlänge, zu ermitteln, wurde die Ebenheit der Oberfläche als positives reelles Vielfaches der Wellenlänge definiert und erhöht. Dieses Vielfache wird der Einfachheit halber als Krümmungskoeffizient C‘ bezeichnet. Dieser Krümmungskoeffizient, der ein Wert ohne Einheit ist, ist nicht mit der Krümmung zu verwechseln, die der Kehrwert des Krümmungsradius ist und eine Längeneinheit hat, wie in Gleichung 1 dargestellt. Die Krümmung kann sich auch über mehrere Größenordnungen erstrecken, während der Krümmungskoeffizient, der eine beliebige positive Zahl sein kann, in der Regel ein Bruch kleiner 1 ist. Somit kann die Sag-Abweichung als die Wellenlänge des Lichts im System, λ, multipliziert mit dem Krümmungskoeffizienten dargestellt werden (Gleichung 7).

(7)\begin{align} C' & \in \mathbb{R}_{\geq 0} \\ \text{SF} \left[ \lambda \right] & = C' \\ \text{SF} \left[ \text{nm} \right] & = C' \times \lambda \end{align}

Die jeweiligen Ergebnisse für drei Wellenlängen und neun Krümmungskoeffizientenwerte sind in Tabelle 1 und Abbildung 2 dargestellt.

	Geometrische Punktgrößen (μm)
Oberflächenebenheit (P-V)	0λ	λ/20	λ/10	λ/8	λ/4	λ/2	1λ	2λ	5λ
1064 nm	22,4	22,9	25,1	26,3	32,0	43,7	67,2	116,4	270,8
532 nm	21,7	21,6	22,3	22,8	25,6	31,3	42,9	66,1	139,0
355 nm	20,7	21,6	21,6	21,9	22,7	26,5	34,1	34,1	96,1

Tabelle 1: Simulierte Punktgrößen bei zunehmender Spiegelkrümmung bei 1064 nm und den ersten beiden Nd:YAG-Harmonischen.

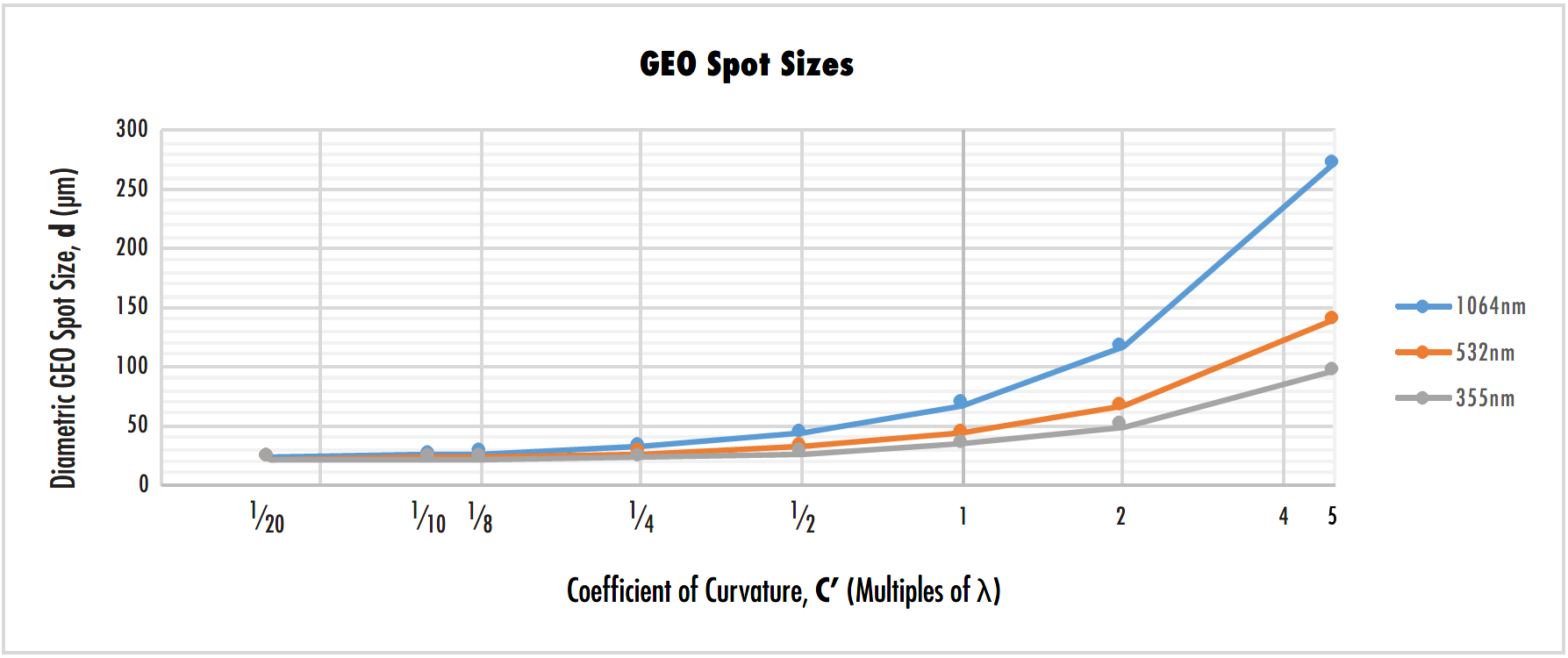
Abbildung 2: Die geometrischen Punktgrößen aus Tabelle 1 werden schnell größer, wenn die Spiegel stärker gekrümmt sind.

Abbildung 2 zeigt, dass die Größe der fokussierten Punkte bei Spiegeln mit einer Oberflächenebenheit von λ/20 für die verschiedenen Wellenlängen fast genau gleich zu sein scheint. Mit schlechterer Ebenheit der Oberfläche werden die fokussierten Punkte für längere Wellenlängen größer. Ab einer Oberflächenebenheit von λ/4 nimmt die Größe des fokussierten Punkts bei allen Wellenlängen merklich zu.

Einflüsse und Hinweise

In der Realität gibt es keine vollkommen flachen Spiegel. Bei niedrigeren Ebenheitsspezifikationen oder höherer Spiegelkrümmung nimmt die Punktgröße zu und die reflektierte Wellenfront verschlechtert sich. Wenn das Oberflächenprofil eines Spiegels erheblich von seiner Nennform abweicht, kann es hilfreich sein, die Aberrationen auf der Oberfläche an eine Reihe von Funktionen, die sogenannten Zernike-Polynome, anzupassen. Je nach Oberflächenprofil des Spiegels und den Winkeln, in denen die Spiegel in Bezug auf den einfallenden Strahl positioniert sind, können Aberrationseffekte von nachkommenden Linsen und Spiegeln konstruktiv oder destruktiv zusammenwirken.

In dieser Simulation wurden der Einfachheit halber nur sphärische oder plane Spiegel verwendet. Infolgedessen sind die Strahlenprofile nicht kreisförmig, sondern eher ausgedehnt. Es ist jedoch wichtig zu beachten, dass ursprünglich in den Strahlaufweitungs- und Strahlfokussierungslinsen sphärische Aberrationen vorhanden waren und die Effekte unweigerlich durch das System getragen und durch die Neigung und sphärische Krümmung der Spiegel verzerrt wurden. Da diese Wechselwirkungen komplex sind und je nach Platzierung der Spiegel additiv oder subtraktiv sein können, war eine Optimierung des Linsenabstands durch OpticStudio erforderlich, um Aberrationseffekte zu minimieren und den Punkt zu fokussieren. Ein weiterer Faktor, der nicht berücksichtigt wurde, ist die Verwendung von optischen Beschichtungen.

Auch darf nicht übersehen werden, wie die Wellenlänge des Lichts in Verbindung mit der Spiegelkrümmung die Größe und Form des Punkts beeinflusst. Bei größeren Wellenlängen sind die Abweichungen in Punktgröße und -form größer und ausgeprägter als bei kürzeren Wellenlängen (Abbildung 3).

Die Größe des fokussierten Punkts bei 1064 nm und zunehmenden Krümmungskoeffizienten auf drei Skalen: 600 μm (oben), 200 μm (Mitte) und 100 μm (unten)

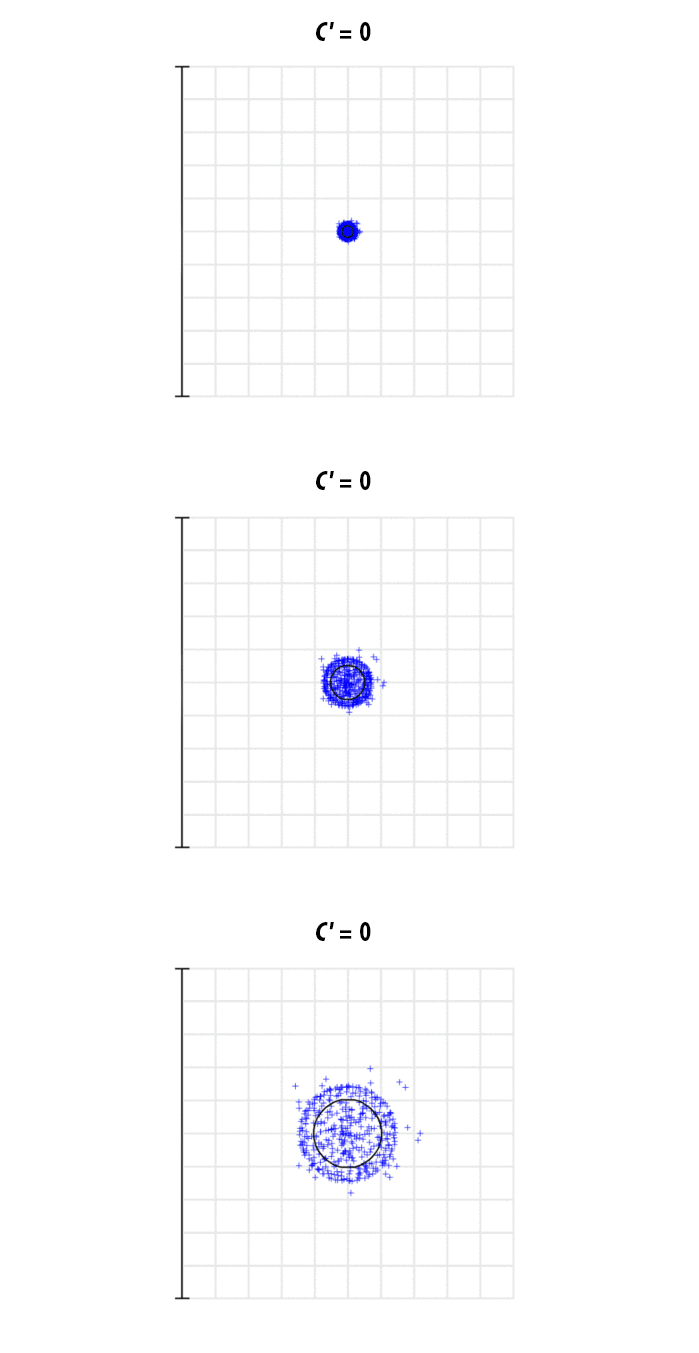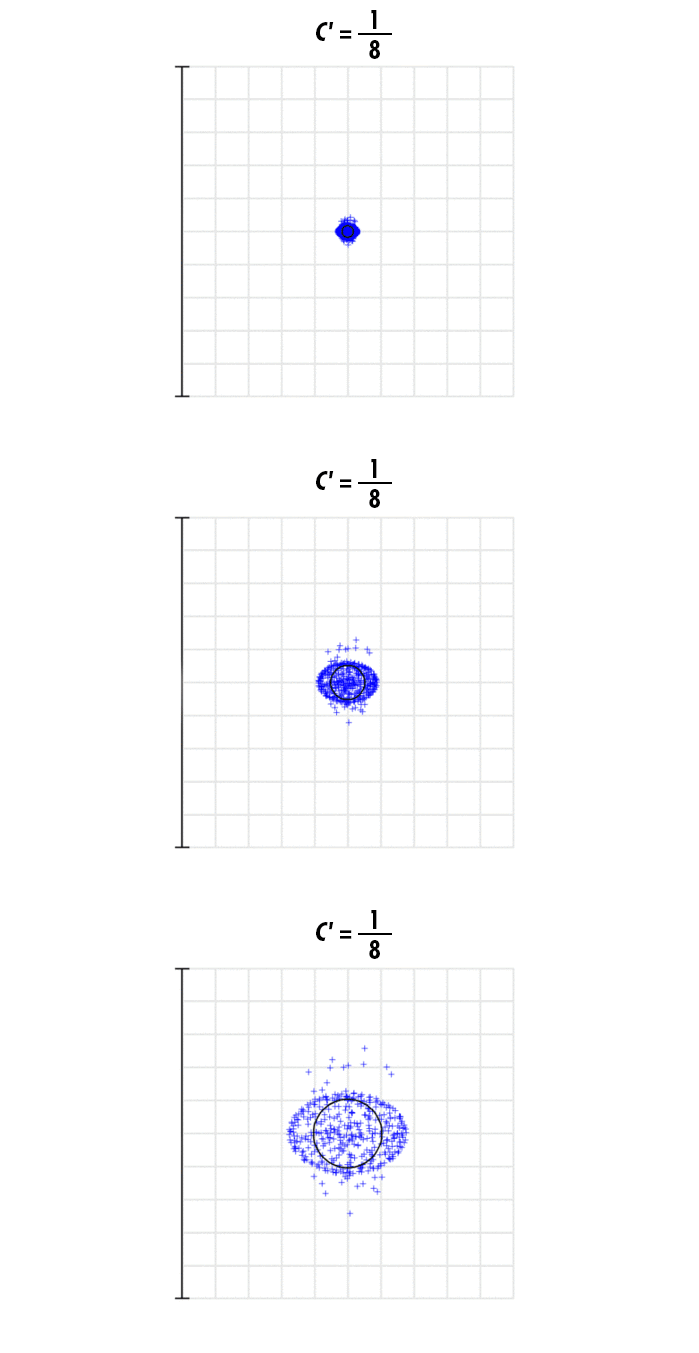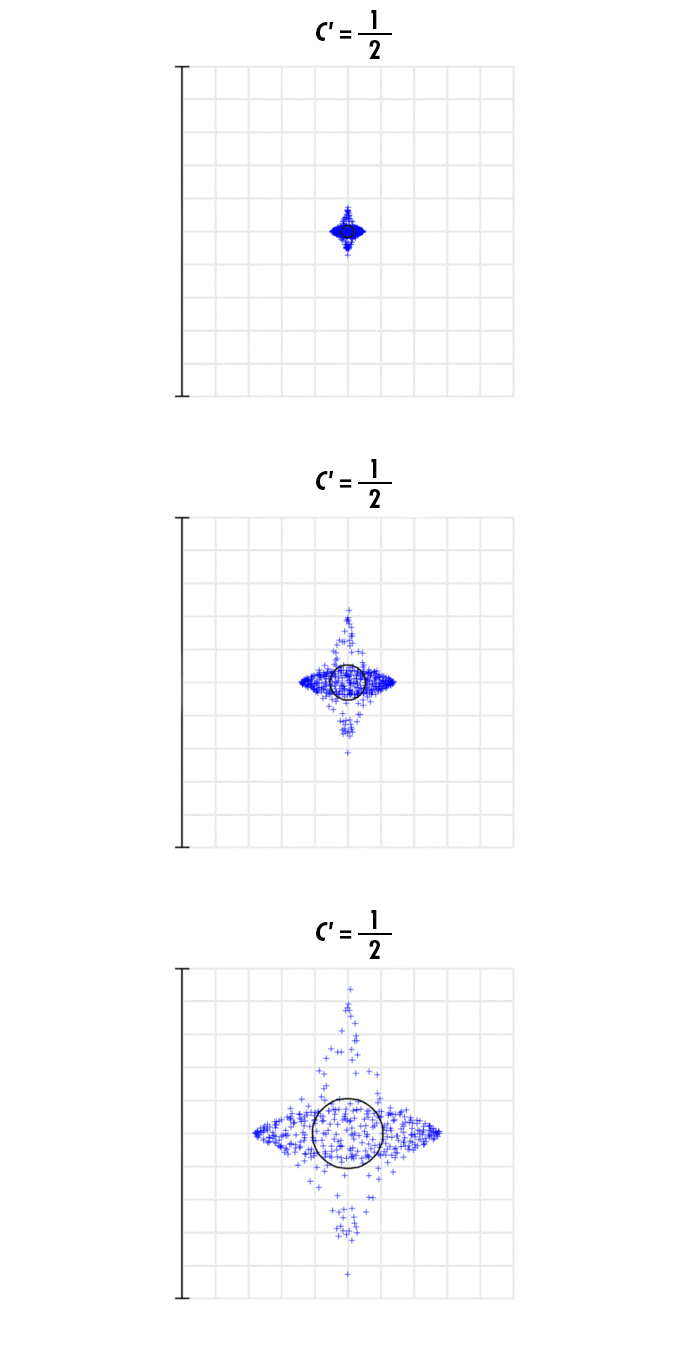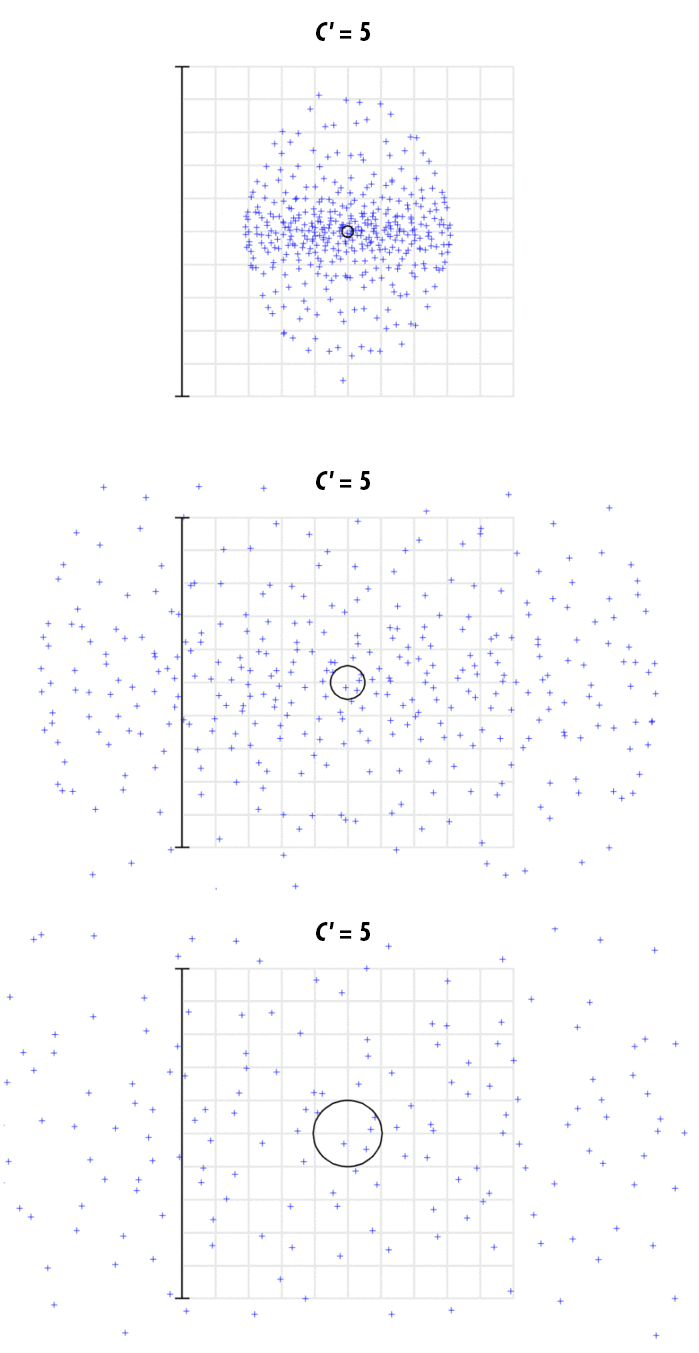
Abbildung 3: Die Größe des fokussierten Punkts bei 1064 nm und zunehmenden Krümmungskoeffizienten auf drei Skalen: 600 μm (oben), 200 μm (Mitte) und 100 μm (unten)

Da es sich um eine rein theoretische Simulation handelt, reflektieren und transmittieren die Spiegel und Linsen jeweils 100% des einfallenden Lichts. In Wirklichkeit verwenden Lasersysteme hochleistungsfähige Reflexionsbeschichtungen, um die Spiegelreflexion zu maximieren, und Antireflexionsbeschichtungen, um die Linsentransmission zu maximieren. Diese Beschichtungen sind jeweils für bestimmte Wellenlängen oder Wellenlängenbereiche geeignet und auch die laserinduzierten Zerstörschwellen (LIDTs) müssen für reale Systeme berücksichtigt werden.

Es ist weiterhin zu beachten, dass eine große Anzahl von Spezifikationen und Faktoren die Systemleistung und die Herstellungskosten beeinflussen können, wie z. B. Beschichtungsarten oder mechanische Spezifikationen wie Parallelität oder Oberflächengenauigkeit. Diese zusätzlichen Faktoren sind bei der Auswahl von Komponenten für ein Lasersystem ebenfalls wichtig, auch wenn viele von ihnen im Rahmen dieser Simulation nicht berücksichtigt wurden.