Anwendungsbeispiele für Optiken
Anwendung 1: Detektorsysteme | Anwendung 2: Auswahl der richtigen Linse | Anwendung 3: Aufbau eines Projektorsystems
Anwendung 1: Detektorsysteme
Jedes optische System erfordert eine gewisse Vorplanung. Die ersten Schritte der Konstruktion sind oft die schwierigsten, wenn jedoch bestimmte wichtige technische Daten des Systems bekannt sind, fällt die Planung leichter. Die folgenden Fragen zeigen, wie eine einzelne Linse zur Lichtsammlung und als Kollimator eingesetzt werden kann.
Zielstellung: Wohin soll das Licht gelangen?
Obwohl Linsen natürlich häufig in abbildenden Systemen zu finden sind, ist in vielen Fällen ihre einzige Aufgabe, Licht von einem Punkt innerhalb eines Systems zu einem Anderen zu projizieren. Fast alle Emitter, Detektoren, Laser und Faseroptiken erfordern diese Art der Stahllenkung. Bevor Sie mit der eigentlichen Konstruktion des Systems beginnen, müssen Sie eine wichtige Frage beantworten: "Wohin soll das Licht gelangen?". Wenn es das Ziel ist, das gesamte einfallende Licht mit so wenig Aberrationen wie möglich auf einen Detektor zu lenken, kann eine einfache Einzellinse, beispielsweise eine plankonvexe Linse (PCX-Linse) oder eine doppelkonvexe Linse (DCX-Linse) verwendet werden.
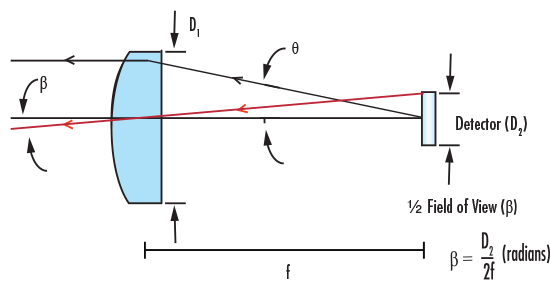
Abb.1: Bildfeldbegrenzung einer PCX Linse in einer Detektoranwendung
Abbildung 1 zeigt eine PCX-Linse mit den beiden entscheidenden technischen Daten: Durchmesser der Linse (D1) und Brennweite (f). Außerdem ist dargestellt, wie der Durchmesser des Detektors das Bildfeld (FOV) des Systems begrenzt. Der Zusammenhang wird näherungsweise durch die Formel
beschrieben. Der exakte Zusammenhang lautet:
Für Detektoren in Scannersystemen ist das wichtigste Maß das Momentanbildfeld (IFOV). Damit wird der Raumwinkel bezeichnet, der in jedem Moment durch den Sensor abgedeckt wird.
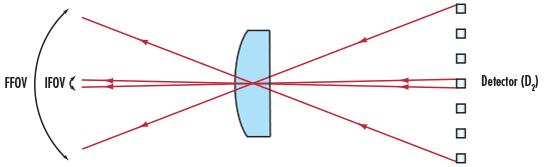
Abb.2: Momentanbildfeld (IFOV)
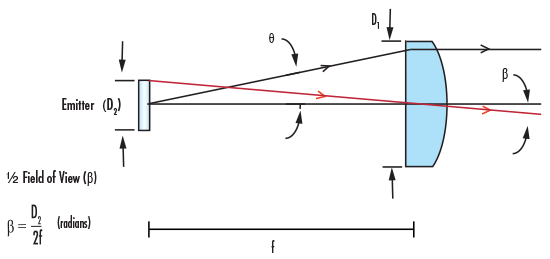
Abb.3: Bildfeldbegrenzung einer PCX-Linse in einer Emitteranwendung
Umgekehrt betrachtet kann Abbildung 1 auch als Darstellung eines Emittersystems interpretiert werden (vgl. Abb.3), wobei die Linse zur Kollimation des Lichts verwendet wird. Diese Konfiguration ist Voraussetzung für das Anwendungsbeispiel.
Lichttransmission: Wie viel Licht gibt es anfänglich?
Wenn Sie wissen, wohin das Licht gelangen soll, haben Sie den ersten Schritt bei der Konstruktion eines Lichtprojektionssystems getan; genauso wichtig ist es aber zu wissen, wie viel Licht von dem Objekt oder der Lichtquelle überhaupt ausgeht. In Detektoraufgaben soll diese Frage beantwortet werden, indem man aus der Lichtintensität auf dem Detektor Rückschlüsse zieht. Dafür ist natürlich entscheidend, ob die Linse überhaupt das komplette Licht einfangen kann. Kenngrößen dafür sind die numerische Apertur NA und die Blendenzahl f/# der Linse, die ihrerseits wieder von der Brennweite f, Durchmesser D, Brechungsindex n und Akzeptanzwinkel θ abhängen.
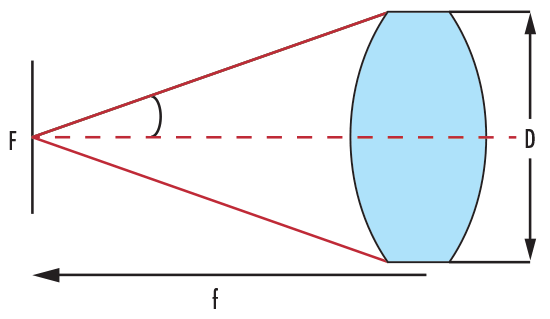
Abb.4: DCX-Linse mit f/# und NA
Die Gleichungen 1.4 und 1.6 definieren die Blendenzahl und die numerische Apertur. Unter Annahme der Kleinwinkelnäherung gilt zwischen beiden Größen zudem der Zusammenhang 1.5. Abbildung 4 soll diese Beziehung veranschaulichen. Je größer der Durchmesser und je kleiner die Blendenzahl f/# ist, desto mehr Licht kann die Linse einfangen. Um ein möglichst effizientes System zu konstruieren, sollte am besten der emittierte Lichtkegel der Quelle mit dem Akzeptanzkegel der Linse übereinstimmen. Damit wird vermieden, dass Licht verloren geht oder die Linse größer ist als notwendig.
Lichtdurchsatz: Wie viel Licht gelangt durch das System?
Wenn eine Linse zur Übertragung von Licht von einer Quelle auf einen Detektor verwendet wird, ist es wichtig, den Lichtdurchsatz (TP), bzw. die Transmission zu kennen. Diese Kenngröße entspricht im Grunde der Antwort auf die Frage "Wie viel Licht gelangt durch das System?". Weil reale Emitter Flächen und keine idealen Punktquellen sind, beeinflusst der Durchmesser einer Linse den optischen Durchsatz selbst dann, wenn die Blendenzahl f/#, also das Verhältnis zwischen Durchmesser und Brennweite, konstant bleibt.
Gleichung 1.7 definiert den Lichtdurchsatz. Hierbei ist A die Fläche des Objekts (Lichtquelle) und Ω der Raumwinkel, unter dem die Linse erscheint. Abbildung 5, die die Zusammenhänge veranschaulicht, zeigt zudem die Objektweite z und die entsprechenden, konjugierten Punkte im Bildraum A', Ω' und z'.
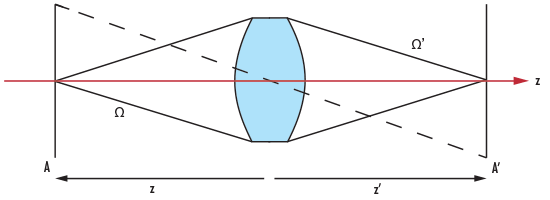
Abb.5: DCX-Linse und Durchsatz
Der Raumwinkel Ω ist definiert als Ω = A/r2, wobei A_L die Linsenfläche ist und der Radius r hier dem Abstand Linse - Objekt entspricht, also r = z (bzw. z' für Ω').
Die Lichtmenge, die auf den Detektor fällt, kann durch Vignettierung reduziert werden. Dabei wird Licht durch physische Begrenzungen des Systems geblockt, zum Beispiel durch die begrenzte Linsenapertur. Einige Systeme nutzen den Vignettierungseffekt gezielt, da dadurch Streulicht eliminiert werden kann, das die Bildqualität beeinträchtigen würde. Es ist zu beachten, dass durch die korrekte Ausrichtung der Komponenten innerhalb des Systems Streulicht und unerwünschte Vignettierung reduziert werden kann.
Aberrationen: Wie sieht das Bild aus?
Die Frage, wie viel Licht durch ein System gelangt, ist wichtig. Strahlaberrationen im System spielen jedoch, vor allem bei abbildenden Systemen, ebenfalls eine entscheidende Rolle. Wenn die Frage "Wie sieht die Abbildung aus?" von Bedeutung für die Funktionalität des Systems ist, dann sind zusätzliche Überlegungen bei der Auslegung des Systems unumgänglich. So können bei entsprechendem Design die auftretenden Aberrationen deutlich reduziert werden, was die Bildqualität verbessert. Aberrationen sind Fehler, die jedes optische System hat, unabhängig von der Präzision der Komponenten und deren Ausrichtung. Der Entwickler steht damit immer vor der wichtigen Aufgabe, ein Gleichgewicht zwischen Kosten und technischen Eigenschaften zu finden. Verschiedene geometrische Aberrationen, beispielsweise Koma (Änderungen des Abbildungsmaßstabs bzw. der Bildgröße mit der Apertur), sphärische Aberration (Lichtstrahlen abseits der optischen Achse fokussieren vor oder hinter dem paraxialen Brennpunkt) und Astigmatismus (ein Brennpunkt für horizontal einfallende Strahlen und ein anderer für vertikal einfallende Lichtstrahlen) können durch eine größere Blendenzahl f/# verringert werden, wie mit den folgenden Gleichungen beschrieben.
Anwendungsbeispiel: Detektorsystem
Angenommen, man hat ein System wie in Abbildung 3, bei dem die Lichtquelle ein Lichtleiter mit einem Durchmesser von ¼" ist.
- Anfangsparameter
Numerische Apertur NA des Lichtleiters = 0,55
Durchmesser des Lichtleiters = 6,35 mm
Brechungsindex von Luft = 1 - Berechnete Parameter
Blendenzahl (f/#)
Eine PCX-Linse mit einer Blendenzahl f/1, das heißt f/# = 1, wäre ideal geeignet, um das Licht des Lichtleiters möglichst vollständig zu kollimieren. Nach Gleichung 1.4 sind, wenn die Blendenzahl f/# = 1 ist, Durchmesser und Brennweite einer Linse gleich. Mit anderen Worten, wenn wir eine Linse mit f/1 und 12 mm Durchmesser haben, beträgt die Brennweite ebenfalls 12 mm.
Volles Bildfeld (FFOV)
Der Raumwinkel wird in Steradiant gemessen. Ein größerer Raumwinkel ergibt sich durch einen kürzeren Abstand zwischen Faser und Linse bzw. einem größeren Durchmesser der Linse. Der größte Wert, den ein Raumwinkel haben kann, ist 4π, bzw. etwa 12,57, dies entspricht einer vollen Kugeloberfläche.
Um den optischen Durchsatz (TP) dieses Systems zu berechnen, müssen wir zunächst die Fläche der Lichtquelle (Gleichung 1.11), die Fläche der Linse (Gleichung 1.12) und den Raumwinkel (Gleichung 1.13) berechnen. Als Faustregel gilt, dass zur Kollimierung von Licht einer divergenten Lichtquelle (beispielsweise des Lichtleiters in diesem Beispiel), diese im Brennpunkt der Linse platziert werden muss.
Da das System sich im freien Raum befindet und n näherungsweise 1 ist, geht n2 als Faktor nicht in die Endberechnung ein.
ANWENDUNG 2: AUSWAHL DER RICHTIGEN LINSE
Eine hohe Bildqualität ist gleichbedeutend mit niedrigen Aberrationen. Infolgedessen nutzen die Konstrukteure oft ein System zwei oder drei Linsen, um eine höhere Bildqualität als mit einer Einzellinse zu erreichen. Bei der Auswahl der richtigen Linse für eine Anwendung spielen viele Faktoren eine Rolle: Art der Lichtquelle, Platzverhältnisse, Kosten usw.
Die Abbildungen 6a bis 6e zeigen die verschiedenen Linsensysteme für eine Relaisoptik, das heißt eine Abbildung im Maßstab 1:1. Anhand der verschiedenen Beispiele zur Auslegung eines solchen Systems, auf die in den folgenden Abschnitten noch näher eingegangen wird, ist sofort zu erkennen, wie die Bildqualität durch die Geometrie und die optischen Eigenschaften der gewählten Linsen verändert wird.
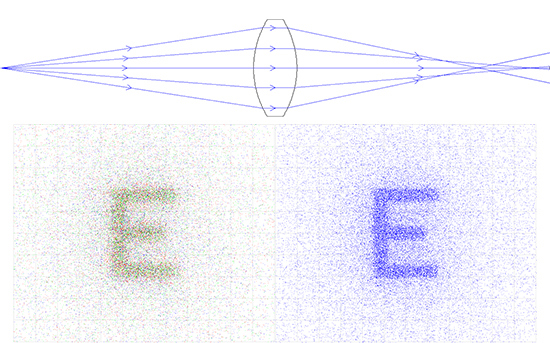
Abb.6a: Relaisoptik mit DCX-Linse: EFL 25 mm x 20 mm Durchmesser der Eintrittspupille (links farbiges und rechts monochromatisches Licht)
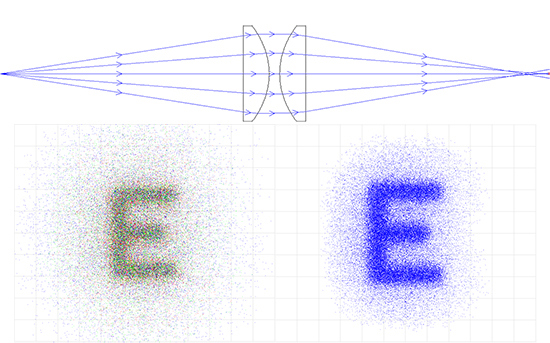
Abb.6b: Relaisoptik mit PCX-Linsen EFL 50 mm x 20 mm Durchmesser der Eintrittspupille (links farbiges und rechts monochromatisches Licht)
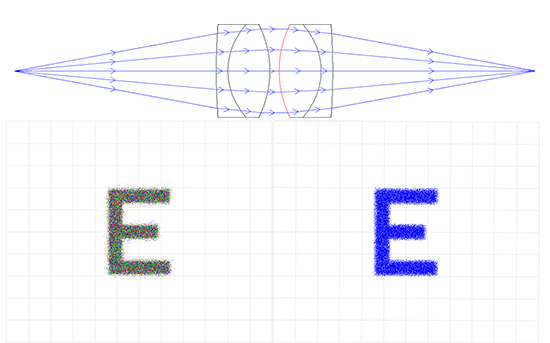
Abb.6c: Relaisoptik mit achromatischen Linsen: EFL 50 mm x 20 mm Durchmesser der Eintrittspupille (links farbiges und rechts monochromatisches Licht)
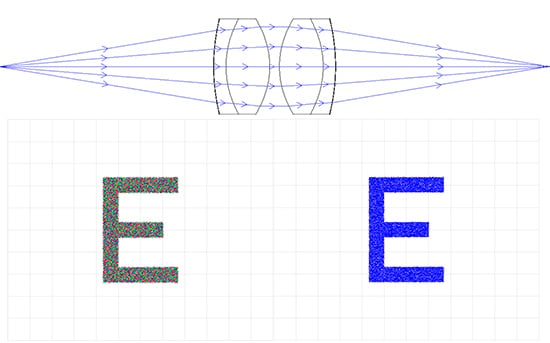
Abb.6d: Relaisoptik mit asphärischen Achromaten: EFL 50 mm x 50 mm Durchmesser der Eintrittspupille (links farbiges und rechts monochromatisches Licht)
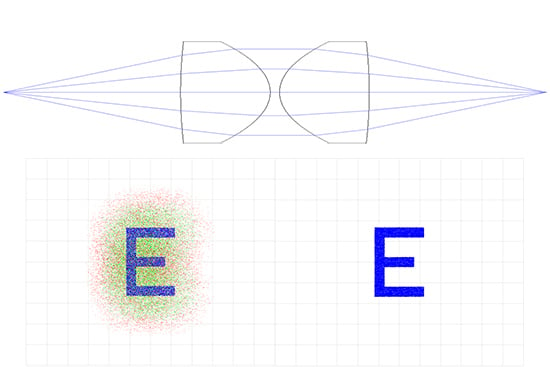
Abb.6e: Relaisoptik mit Asphären: EFL 50 mm x 40 mm Durchmesser der Eintrittspupille (links farbiges und rechts monochromatisches Licht)
Anwendungsbeispiel: System mit Einzellinse
Die beste Einzellinse für eine 1:1 Abbildung ist die doppelkonvexe Linse (DCX-Linse). Hauptgrund dafür ist die symmetrische Form. Im Gegensatz zu einer plankonvexen Linse haben beide Seiten dieselbe Brechkraft, was für die ebenfalls symmetrische 1:1-Abbildung Vorteile bringt. Da nur eine einzelne Linse Verwendung findet, ist die effektive Blende gleich der Linsenapertur, was einige Aberrationen reduziert. Damit ist zwar festzuhalten, dass für eine 1:1-Abbildung eine doppelkonvexe Linse (DXC-Linse) einer einzelnen plankonvexen Linse (PCX-Linse) vorzuziehen ist, allerdings treten bei kleinen Blendenzahlen noch signifikante sphärische Aberrationen und Koma auf. Diese Aberrationen werden durch den Formfaktor S der Einzellinse verursacht
wobei R1 und R2 die Radien der jeweiligen Linsenflächen sind.
Für Anwendungen, bei denen das Objekt bzw. die Lichtquelle unendlich weit entfernt sind, ist nur eine Linse notwendig. In diesem Fall kann der Formfaktor recht einfach so berechnet werden, dass die störendsten Aberrationen reduziert werden. Beispielsweise kann zur Abschwächung der sphärischen Aberration der ideale Formfaktor wie folgt berechnet werden:
Hierbei ist n der Brechungsindex der verwendeten Glassorte, p der Positionsfaktor, z die Objektweite (als negativer Wert gemessen) und z' die Bildweite (als positiver Wert gemessen).
Um bei unendlicher Objektweite Koma zu reduzieren, kann der Formfaktor wie folgt berechnet werden:
Bei Glas mit einem Brechungsindex von 1,5 (N-BK7 hat den Brechungsindex 1,517) und einem Objekt bei unendlich, bietet ein Formfaktor von 0,8 die beste Balance zwischen sphärischer Aberration und Koma.
Anwendungsbeispiel: System mit zwei Linsen
Um die Eigenschaften des Systems zu verbessern, kann die einzelne DCX-Linse durch zwei identische PCX-Linsen und eine Blende zwischen den Linsen ersetzt werden. Die Brennweite muss doppelt so groß gewählt werden, wie die der DCX-Linse. Damit wird die Brechkraft der einen DCX-Linse auf die beiden PCX-Linsen aufgeteilt, da die Brennweite umgekehrt proportional zur Brechkraft ist. Da jede Linse eine geringere Brechkraft aufweist, ergibt sich in dem System eine geringere sphärische Aberration, obwohl die Gesamtbrennweite konstant bleibt. Da der Durchmesser ebenfalls gleich geblieben ist, ändert sich die Blendenzahl f/# nicht, wenn statt einer einzelnen DCX-Linse zwei PCX-Linsen verwendet werden. Die sphärische Aberration reduziert sich jedoch auch bei einer großen Blendenzahl f/#.
Die konvexen Oberflächen sollten möglichst nahe zusammen stehen, die Blende liegt dazwischen. Allgemein sollte die konvexe Seite der Linse in Richtung des größeren der beiden Abstände (Objekt- / Bildweite) zeigen, um die bestmögliche Bildqualität zu erzielen.
Anwendungsbeispiel: Optisches System mit Achromat
Eine andere Möglichkeit ist die Verwendung von zwei achromatischen Linsen oder Achromaten. Eine achromatische Linse besteht aus zwei optischen, miteinander verkitteten Komponenten, in der Regel einer positiven Konvexlinse mit niedrigem Brechungsindex (Kronglas) und einer negativen Konkavlinse mit hohem Brechungsindex (Flintglas). Bei Verwendung von Achromaten verringert sich die chromatische Aberration, also Abbildungsfehler bei der Verwendung mehrer Wellenlängen, wie es zum Beispiel bei weißem Licht der Fall ist. Die Fehler entstehen durch die Dispersion des verwendeten Glases, da der Brechungsindex und damit auch die Brechkraft von der Wellenlänge abhängen. Auch die sphärische Aberration und Koma werden im Vergleich zu gewöhnlichen Linsen reduziert. Zwei Achromate, deren konvexe Seiten zueinander zeigen, erzeugen eine deutlich bessere Abbildung, als die bisher diskutierten Systeme. Die sphärische Aberration ist bei großen Aperturen oder hohen Blendenzahlen f/# vernachlässigbar, die chromatische Aberration wird durch Verwendung von Achromaten deutlich reduziert. Viele Relaisoptiken auf dem Markt nutzen diese Konfiguration mit vier Elementen.
Weitere Informationen über die Vorteile achromatischer Linsen im Vergleich zu Einzellinsen finden Sie in dem Abschnitt Gründe für achromatische Linsen.
Anwendungsbeispiel: System mit asphärischer Linse
Im Gegensatz zu PCX-, DCX- und achromatischen Linsen, die alle sphärisch sind, also Ausschnitte einer Kugel darstellen, ist eine asphärische Linse eine Linse, deren Krümmung nicht konstant ist. Die Oberfläche besteht, vereinfacht gesagt, aus Abschnitten einer Hyperbel oder Parabel. Das Kernkonzept von asphärischen Linsen oder Asphären ist eine Veränderung des Krümmungsradius radial zur optischen Achse. Damit lassen sich sphärische Aberrationen bequem korrigieren. Außerdem eignen sich Asphären gut zur Korrektur von sonstigen Aberrationen abseits der optischen Achse.
Asphären werden in vielen Systemen eingesetzt. Eine asphärische Linse kann zwei oder mehr sphärische Linsen ersetzen und verringert somit den Platzbedarf und die Gesamtkosten eines Systems. Weitere Informationen über die Herstellung, Konstruktion und den Einsatz von Asphären finden Sie im Abschnitt Alles über Asphären.
| Art des Linsensystems | Sphärische Aberration | Chromatische Aberration |
|---|---|---|
| DCX-Einzellinse | Hoch | Hoch |
| 2 PCX-Linsen | Mittel | Hoch |
| 2 Achromate | Niedrig | Vernachlässigbar |
| 2 Asphärische Achromate | Vernachlässigbar | Vernachlässigbar |
ANWENDUNG 3: AUFBAU EINES PROJEKTORSYSTEMS
Die Konstruktion eines eigenen Projektorsystems kann oft zeitraubend und kostspielig sein. Wenn einige einfache Schritte eingehalten werden, wird die Konstruktion einfacher und effizienter. Der folgende Plan kann für sehr viele, verschiedene Designaufgaben verwendet werden.
Schritte für eine benutzerdefinierte Konstruktion:
- Unterteilen Sie das System in Module – Es gibt viele unterschiedliche Anwendungen, von einfachen Lupen bis zur Laserstrahl-Formung. Die meisten Systeme können Sie jedoch in kleinere Module aufteilen, die dann unabhängig voneinander entwickelt werden können.
- Konstruieren Sie jedes Teil separat – Wenn jedes Modul für sich optimiert wird, kann das gut für die Leistung des Gesamtsystems sein. Allerdings gibt es auch Situationen, in denen einzelne Module konkurrierende Anforderungen haben und die Faktoren ausbalanciert werden müssen. Die komponentenweise Konstruktion ist trotzdem ein guter Ansatzpunkt, solange man das Gesamtsystem nicht komplett aus den Augen verliert.
- Optimierung am Computer – Nachdem ein grundlegendes Konzept als Ausgangspunkt gewählt wurde, lassen sich die einzelnen Module und das komplette System am einfachsten mit einer geeigneten Optikdesign-Software, wie Zemax oder Code V, optimieren. Das so gefundene Layout ist dann der Ausgangspunkt für das vorläufige mechanische Design und die Prototypen.
- Aufbau des Systems – Nachdem die Module aufgebaut sind, sollte jedes einzeln auf seine Funktion hin überprüft werden. Erst danach wird das Gesamtsystem zusammengesetzt. Um mögliche Fehler zu erkennen, kann das System nochmal in der Designsoftware simuliert und die Messergebnisse mit den theoretischen Eckdaten verglichen werden.
- Auswahl von Teilen – Die meisten Softwarepakete für das Optikdesign enthalten eine Bibliothek mit schnell verfügbaren Standardlinsen und einem Algorithmus, der die theoretisch ermittelten Linsen mit dieser Auswahl abgleicht und die sinnvollste Alternative sucht. Die Software kann bei der Optimierung zum Beispiel ein Glas liefern, das so einfach nicht erhältlich ist. Mit dem Algorithmus kann dieses dann mit den realen Gläsern abgegelichen und ein geeigneter Ersatz gefunden werden. Sie müssen nicht nur die richtigen Gläser auswählen, sondern auch die passende Mechanik für das System finden. Sie müssen Größe, Gewicht und Aussehen berücksichtigen, bevor Sie Linsenfassungen und Systemhalterungen auswählen.
Weitere Informationen zur Glasauswahl finden Sie im Abschnitt Optische Gläser.
Die meisten Projektoren, wie die altbekannten Diaprojektoren, lassen sich in zwei Module unterteilen: Das Kondensorlinsensystem und das Projektorlinsensystem. Der Kondensor leuchtet ein Dia gleichmäßig aus; das Projektorlinsensystem projiziert das Bild dann auf einen Schirm. Beide Module können mit einfachen Komponenten und grundlegenden Techniken aufgebaut werden. In diesem Beispiel werden Optiken mit 25 mm Durchmesser verwendet, weil sie eine große Apertur besitzen und eine sehr große Auswahl an Brennweiten erhältlich ist.
Teil 1: Das Projektorsystem
Der Aufbau des Projektorsystems wird durch die gewünschte Vergrößerung und den Projektionsabstand des Objekts, hier eine Strichplatte, bestimmt. Da die meisten Projektorsysteme mit weißem Licht arbeiten, erzielen Sie die besten Bilder bei Verwendung achromatischer Linsen. Für die Auswahl der achromatischen Linsen müssen Sie wissen, wie weit vom projizierten Bild entfernt sich das Projektorlinsensystem (I) befinden soll, und wie groß der gewünschte Abbildungsmaßstab (M) sein soll. Der Abbildungsmaßstab kann aus den Brennweiten der Linsen (Gleichung 3.1) bzw. aus der Entfernung zwischen Bild und Objekt (Gleichung 3.2) berechnet werden.
Teil 2: Das Kondensor-Linsensystem
Das Kondensorlinsensystem sammelt das Licht divergenter Lichtquellen und lenkt das Licht dann über das Objekt zum Projektorlinsensystem. Das klassische Kondensorlinsensystem besteht aus zwei PCX-Linsen, die so montiert sind, dass die konvexen Seiten zueinander zeigen, siehe dazu Abbildung 7. Die erste Linse bündelt den divergenten Lichtkegel der Lichtquelle (Objekt oder Projektor), die zweite Linse gibt das Licht als konvergenten Kegel (Bild) aus, der die Strichplatte ausleuchtet.
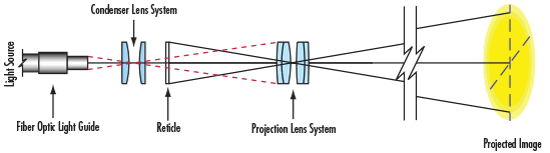
Abb.7: Einfaches Projektorsystem
Das Design des Projektorsystems beeinflusst in diesem Fall auch die Auslegung des Kondensorsystems. Aus diesem Grund ist es entscheidend, dass Sie zuerst das Projektorlinsensystem konstruieren. Der Abstand zwischen dem Kondensorlinsensystem und dem Projektorlinsensystem ist mindestens so groß wie der Abstand zwischen der Strichplatte und dem Projektorlinsensystem.
Anwendungsbeispiel: Konstruktion eines Projektorsystems
- Anfangsparameter
Durchmesser der Linse = 25 mm
Bildabstand = Projektionsabstand = 250 mm
Vergrößerung = 2,5X - Berechnete Parameter
Objektentfernung bzw. Abstand zur Strichplatte
Zwei achromatische Linsen mit 100 mm Brennweite und einem Durchmesser von 25 mm wären für den Aufbau des Projektorlinsensystems ideal geeignet. Linsen mit einem Durchmesser von 25 mm sind aufgrund ihrer großen Aperturen und der Kompatibilität mit den mechanischen Teilen ideal geeignet, ebenso aufgrund der Vielzahl von Beschichtungen und Brennweiten.
Brennweite der PCX-Kondensorlinse
Zum Aufbau des Projektorsystems werden zwei PCX-Linsen mit einer Brennweite von 250 mm und einem Durchmesser von 25 mm benötigt.































































weitere regionale Telefonnummern
ANGEBOTSTOOL
Geben Sie zum Starten die Produktnummer ein.
Copyright 2023 | Edmund Optics Inc. vertreten durch Edmund Optics GmbH, Isaac-Fulda-Allee 5, 55124 Mainz, Deutschland
Die Edmund Optics GmbH Deutschland fungiert als Handelsvermittler für die Edmund Optics Ltd. in Großbritannien.
Vertragspartner ist die Edmund Optics Ltd. in Großbritannien.